Zum Inhalt springen

Teil A - Pflichtaufgaben

Version 14.2 von Holger Engels am 2024/12/15 17:13

Gegeben ist eine im Intervall \([-4;4]\) definierte Polynomfunktion f vom Grad 3. Der Graph von f ist punktsymmetrisch zum Ursprung und schneidet die x-Achse im Punkt \(N(4|0)\). Der Wertebereich von f ist \(W_f=[-2;2]\).

  1. Skizziere den Graphen der Funktion f, wenn bekannt ist, dass \(f'(0)<0\) gilt. [3 BE]
  2. Bestimme eine Funktionsgleichung einer trigonometrischen Funktion g, sodass f und g im Intervall \([-4;4]\) dieselben Nullstellen haben. [2 BE]
AFB   IIIKompetenzen   k.A.Bearbeitungszeit   15 min
Quelle   Abitur 2024Lizenz   k.A.

Gegeben ist die in ℝ definierte Funktion f mit \(f(x)=-2x+e^{ex}\).

  1. Gib eine Gleichung der Asymptote des Graphen von f an. [1 BE]
  2. Bestimme den x-Wert, an dem der Graph von f die Steigung 2 hat. [2 BE]
  3. Zeige, dass der Graph von f keinen Wendepunkt hat. [2 BE]
AFB   IIIKompetenzen   k.A.Bearbeitungszeit   15 min
Quelle   Abitur 2024Lizenz   k.A.

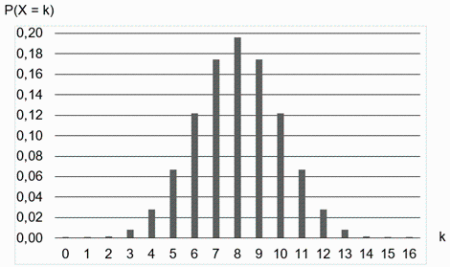UrneWahrscheinlichkeitsverteilung.pngEine Urne enthält 15 weiße und 15 rote Kugeln. Aus dieser wird 16-mal mit Zurücklegen gezogen. Die Zufallsvariable \(X\) gibt die Anzahl der gezogenen weißen Kugeln an. Die Abbildung zeigt die Wahrscheinlichkeitsverteilung von \(X\).

  1. Gib den Erwartungswert von \(X\) an. [1 BE]
  2. Bestimme mit Hilfe von Werten aus der Abbildung näherungsweise die Wahrscheinlichkeit \(P(6\leq X\leq 7)\). [2 BE]
  3. Die Zufallsvariable \(Y\) gibt die Anzahl der gezogenen roten Kugeln an. Erläutere, warum die Wahrscheinlichkeitsverteilung von \(Y\) ebenfalls durch die Abbildung oben dargestellt werden kann. [2 BE]
AFB   k.A.Kompetenzen   k.A.Bearbeitungszeit   15 min
Quelle   Abitur 2024Lizenz   k.A.

Gegeben sind die Punkte \(A(1|3|3),B(9|-1|-5),C(3|5|-5)\) und \(M(5|1|-1)\).

  1. Weise folgende Sachverhalte nach [2 BE]:
    1. Der Punkt \(M\) ist der Mittelpunkt der Strecke \(AB\).
    2. Die Vektoren \(\overrightarrow{AM}\) und \(\overrightarrow{MC}\) schließen einen rechten Winkel ein.
  2. Bestimme die Koordinaten eines Punktes, der doppelt so weit vom Punkt \(M\) entfernt ist wie vom Punkt \(C\)  [3 BE].
AFB   k.A.Kompetenzen   k.A.Bearbeitungszeit   15 min
Quelle   Abitur 2024Lizenz   k.A.
K1K2K3K4K5K6
I000000
II000000
III000000