Zum Inhalt springen

Lösung Aufgabe 1

Zuletzt geändert von akukin am 2024/12/28 18:35

Teilaufgabe a)

Erwartungshorizont (offiziell)

K_1 verläuft vom 3. in den 4. Quadranten. Da der Koeffizient der höchsten Potenz von x im Funktionsterm von f positiv ist, stimmt das globale Verhalten von K_1 nicht mit dem von K überein.

K_3 ist achsensymmetrisch zur y-Achse. Da der Funktionsterm von f sowohl gerade als auch ungerade Potenzen von x aufweist, stimmt das Symmetrieverhalten von K_3 nicht mit dem von K überein.

K_2 verläuft vom 2. in den 1. Quadranten. K_2 ist weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Ursprung. Somit stimmen sowohl das globale Verhalten als auch das Symmetrieverhalten von K_2 mit dem von K überein.
Erläuterung der Lösung Aufgabenstellung

Einer der drei Graphen entspricht K. Beurteile für jeden Graph, ob es sich um K handeln kann. GraphKOptionen.png

Lösung

K_1 verläuft vom 3. in den 4. Quadranten. Da der Koeffizient der höchsten Potenz von x im Funktionsterm von f positiv ist, stimmt das globale Verhalten von K_1 nicht mit dem von K überein.

K_3 ist achsensymmetrisch zur y-Achse. Da der Funktionsterm von f sowohl gerade als auch ungerade Potenzen von x aufweist, stimmt das Symmetrieverhalten von K_3 nicht mit dem von K überein.

K_2 verläuft vom 2. in den 1. Quadranten. K_2 ist weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Ursprung. Somit stimmen sowohl das globale Verhalten als auch das Symmetrieverhalten von K_2 mit dem von K überein.

Teilaufgabe b)

Erwartungshorizont (offiziell)

f(x)=\frac{1}{12}x^4-\frac{1}{3}x^3+\frac{4}{3};\ \ f^\prime\left(x\right)=\frac{1}{3}x^3-x^2;\ \ f^{\prime\prime}(x)=x^2-2x;\ \ f^{\prime\prime\prime}(x)=2x-2

f^\prime(x)=0\ \ \Leftrightarrow\ \ \frac{1}{3}x^3-x^2=0\ \ \Leftrightarrow\ \ x^2\left(\frac{1}{3}x-1\right)=0\ \ \Leftrightarrow\ \ x=0\ \ \vee\ \ x=3

f^\prime(0)=0\ \land \ f^{\prime\prime}\left(0\right)=0 \ \land \ f^{\prime\prime\prime}(0)\neq0 \ \land \ f(0)=\frac{4}{3}\ \ \Rightarrow\ \ \text{Sattelpunkt} \ S\left(0\middle|\frac{4}{3}\right)

f^\prime(3)=0\ \land \ f^{\prime\prime}\left(3\right)=3 > 0 \ \ \land \ f(3)=-\frac{11}{12}\ \ \Rightarrow\ \ \text{Tiefpunkt} \ T\left(3\middle|-\frac{11}{12}\right)
Erläuterung der Lösung Aufgabenstellung

Berechne die Koordinaten aller Punkte, an denen K eine waagrechte Tangente hat. Gib für jeden dieser Punkte an, ob es sich um einen Hoch-, Tief- oder Sattelpunkt handelt.

Lösung
Neben der Funktionsgleichung von f werden für diese Teilaufgabe auch die Gleichungen der ersten, zweiten und dritten Ableitungsfunktion benötigt:

f(x)=\frac{1}{12}x^4-\frac{1}{3}x^3+\frac{4}{3};\ \ f^\prime\left(x\right)=\frac{1}{3}x^3-x^2;\ \ f^{\prime\prime}(x)=x^2-2x;\ \ f^{\prime\prime\prime}(x)=2x-2

An Extremstellen ist die erste Ableitung Null, da dort eine waagrechte Tangente angelegt werden kann:

f^\prime(x)=0\ \ \Leftrightarrow\ \ \frac{1}{3}x^3-x^2=0\ \ \Leftrightarrow\ \ x^2\left(\frac{1}{3}x-1\right)=0\ \ \Leftrightarrow\ \ x=0\ \ \vee\ \ x=3

Mit Hilfe der zweiten und gegebenenfalls dritten Ableitung lässt sich überprüfen, ob diese Stellen Hochstellen, Tiefstellen oder Sattelstellen sind. Die y-Koordinate erhält man, wenn man den x-Wert in den Funktionsterm einsetzt.
f^\prime(0)=0\ \land \ f^{\prime\prime}\left(0\right)=0 \ \land \ f^{\prime\prime\prime}(0)\neq0 \ \land \ f(0)=\frac{4}{3}\ \ \Rightarrow\ \ \text{Sattelpunkt} \ S\left(0\middle|\frac{4}{3}\right)
(Ist an einer Stelle die erste und zweite Ableitung Null, die dritte aber nicht Null, so handelt es sich um eine Terrassenstelle/Sattelstelle.)
f^\prime(3)=0\ \land \ f^{\prime\prime}\left(3\right)=3 > 0 \ \ \land \ f(3)=-\frac{11}{12}\ \ \Rightarrow\ \ \text{Tiefpunkt} \ T\left(3\middle|-\frac{11}{12}\right)
(Ist an einer Stelle die erste Ableitung Null und die zweite Ableitung positiv, d. h. der Graph dort linksgekrümmt, so handelt es sich um eine Tiefstelle.)

Teilaufgabe c)

Erwartungshorizont (offiziell) f(2)=\frac{4}{3}-\frac{8}{3}+\frac{4}{3}=0
Erläuterung der Lösung Aufgabenstellung

Weise nach, dass f bei x=2 eine Nullstelle hat.

Lösung
Dass x=2 eine Nullstelle ist, lässt sich am einfachsten überprüfen, wenn man x=2 in den Funktionsterm einsetzt:
f(2)=\frac{4}{3}-\frac{8}{3}+\frac{4}{3}=0

Teilaufgabe d)

Erwartungshorizont (offiziell)

Wendetangente in x=0: t_0(x)=\frac{4}{3}

Wendetangente in x=2: t_2(x)=f^\prime(2)\cdot(x-2)+f(2);\ \ t_2(x)=-\frac{4}{3}x+\frac{8}{3}

t_0(1)=t_2(1)=\frac{4}{3}.
Also ist P Schnittpunkt der beiden Wendetangenten.
Erläuterung der Lösung Aufgabenstellung

Neben dem Wendepunkt W\left(2\middle|0\right) besitzt K einen weiteren Wendepunkt S\left(0\middle| f(0)\right). Der Punkt P\left(1|\frac{4}{3}\right) liegt oberhalb des Graphen von f.
Weise nach, dass sich die beiden Wendetangenten im Punkt P schneiden.

Lösung
Hier empfiehlt es sich, eine Skizze anzufertigen:
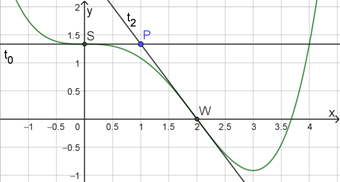
1d)Hinweis2.png

Die Wendetangente in x=0 ist eine waagrechte Gerade, da S ein Sattelpunkt ist: t_0(x)=\frac{4}{3}

Die Wendetangente in x=2 kann mit Hilfe der allgemeinen Tangentengleichung beschrieben werden (siehe Merkhilfe):

t_2(x)=f^\prime\left(2\right)\cdot\left(x-2\right)+f\left(2\right);\ \ t_2(x)=-\frac{4}{3}x+\frac{8}{3}

Wenn sich beide Tangenten in P schneiden, muss die x-Koordinaten von P eingesetzt in die Tangentengleichungen beide Male die y-Koordinate von P ergeben:
t_0(1)=t_2(1)=\frac{4}{3}.
Also ist P Schnittpunkt der beiden Wendetangenten.

Teilaufgabe e)

Erwartungshorizont (offiziell)

Flächeninhalt des gesamten Dreiecks PSW: A_g=\frac{1}{2}\cdot\left|\overrightarrow{SP}\right|\cdot\left|\overrightarrow{SO}\right|=\frac{1}{2}\cdot1\cdot\frac{4}{3}=\frac{2}{3}

Flächeninhalt des Teils des Dreiecks PSW, der unterhalb von K liegt:

\begin{align*} A_u &=\int_{0}^{2}{f(x)\mathrm{d} x}-A_{\mathrm{\Delta}_{OWS} } \\ &=\int_{0}^{2}{\left(\frac{1}{12}x^4-\frac{1}{3}x^3+\frac{4}{3}\right)\mathrm{d} x}-\frac{1}{2}\cdot2\cdot\frac{4}{3}=\left[\frac{1}{60}x^5-\frac{1}{12}x^4+\frac{4}{3}x\right]_0^2-\frac{4}{3}=\frac{28}{15}-\frac{4}{3}=\frac{8}{15} \end{align*}

Flächeninhalt des oberen Teils des Dreiecks PSW: A_o=A_g-A_u=\frac{2}{15}
Erläuterung der Lösung Aufgabenstellung

Das Dreieck PSW wird von K in zwei Teile geteilt. Berechne den Flächeninhalt der Teilfläche oberhalb von K.

Lösung
Auch hier kann eine Skizze sinnvoll sein. Gesucht ist der Inhalt der roten Teilfläche:
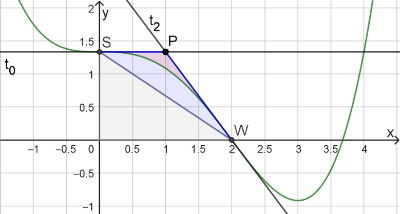
1e)Hinweis1.png
Das blaue Dreieck PSW hat die Grundlinie SP und die Höhe SO (O ist der Ursprung des Koordinatensystems). Flächeninhalt des gesamten blauen Dreiecks PSW ist also:

A_g=\frac{1}{2}\cdot\left|\overrightarrow{SP}\right|\cdot\left|\overrightarrow{SO}\right|=\frac{1}{2}\cdot1\cdot\frac{4}{3}=\frac{2}{3}

Der Flächeninhalt des Teils des Dreiecks PSW, der unterhalb des Graphen von f liegt, ist das Integral von 0 bis 2, aber ohne den Flächeninhalt des grauen Dreiecks OWS:

\begin{align*} A_u &=\int_{0}^{2}{f(x)\mathrm{d} x}-A_{\mathrm{\Delta}_{OWS} } \\ &=\int_{0}^{2}{\left(\frac{1}{12}x^4-\frac{1}{3}x^3+\frac{4}{3}\right)\mathrm{d} x}-\frac{1}{2}\cdot2\cdot\frac{4}{3}=\left[\frac{1}{60}x^5-\frac{1}{12}x^4+\frac{4}{3}x\right]_0^2-\frac{4}{3}=\frac{28}{15}-\frac{4}{3}=\frac{8}{15} \end{align*}


Der Flächeninhalt des roten, oberen Teils des Dreiecks PSW ist also:
A_o=A_g-A_u=\frac{2}{15}