Lösung Stochastik

Zuletzt geändert von akukin am 2025/08/16 10:09

Teilaufgabe a)

Erwartungshorizont(offiziell)

\(P(E_1 )=0,91^{19}\cdot 0,09\approx 0,015\)
\(X\): Anzahl der Testpersonen, die das Produkt vertragen.
\(X\) ist binomialverteilt mit \(n=20\) und \(p=0,91\).
\(P(E_2)=P(X=18)\approx 0,282\)
\(0,7\cdot 20=14\)
\(P(E_3 )=P(X\geq 14)=1-P(X\leq 13)\approx 1-0,0013\approx 0,9987\)

Erläuterung der Lösung

Aufgabenstellung
Es werden nacheinander 20 zufällig ausgewählte Testpersonen befragt.
Berechne für die folgenden Ereignisse jeweils die Wahrscheinlichkeit:
\(E_1\): Nur die dritte Testperson verträgt das Produkt nicht.
\(E_2\): Genau 18 Testpersonen vertragen das Produkt.

\(E_3\): Mindestens 70% der Testpersonen vertragen das Produkt.

Lösung
\(E_1\): Die erste Person verträgt das Produkt, die zweite auch, die dritte nicht, aber alle nachfolgenden schon.

\(P(E_1 )=0,91\cdot 0,91\cdot 0,09\cdot 0,91\cdot 0,91 \cdots =0,91^{19}\cdot 0,09\approx 0,015\)

\(E_2\): Die Zufallsgröße \(X\): „Anzahl der Testpersonen, die das Produkt vertragen“ ist binomialverteilt mit \(n=20\) und \(p=0,91\).
\(P(E_2 )=P(X=18)\approx 0,282\) (Taschenrechner: binomialpdf)

\(E_3\): Zuerst muss berechnet werden, wie viel 70% von 20 Personen ist.
\(0,7\cdot 20=14\)
\(P(E_3 )=P(X\geq 14)\)
Da der Taschenrechner nur \(P(X\leq m)\) berechnen kann, also über alle \(P(X=k)\) von \(k=0\) bis \(k=m\) aufsummiert, muss \(P(X\geq 14)\) noch umformuliert werden.
\(P(E_3 )=P(X\geq 14)=1-P(X\leq 13)\approx 1-0,0013\approx 0,9987\) (Taschenrechner: binomialcdf)

Teilaufgabe b)

Erwartungshorizont(offiziell)

\(Y\): Anzahl der Personen, die das Produkt nicht vertragen.
\(Y\) ist binomialverteilt mit \(n=200\) und \(p=0,09\).
\(\mu=18\)
\(P(14\leq Y \leq 22)=P(Y\leq 22)-P(Y\leq 13)\approx 0,8657-0,1308 \approx 0,735\)

Erläuterung der Lösung

Aufgabenstellung

200 Personen nutzen das Pflegeprodukt.
Berechne die Wahrscheinlichkeit, dass dabei die Anzahl der Personen, die das Produkt nicht vertragen, zwischen 14 und 22 liegt.

Lösung
\(Y\): Anzahl der Personen, die das Produkt nicht vertragen. (Binomialverteilt mit \(n=200,\ p=0,09\))
Gesucht ist \(P(14\leq Y\leq 22)\).
Da der Taschenrechner nur \(P(X\leq m)\) berechnen kann, also über alle \(P(X=k)\) von \(k=0\) bis \(k=m\) aufsummiert, muss \(P(14\leq Y\leq 22)\) noch umformuliert werden.
\(P(14\leq Y\leq 22)=P(Y \leq 22)-P(Y\leq 13)\approx 0,8657-0,1308\approx 0,735\)

Teilaufgabe c)

Erwartungshorizont(offiziell)

	\(A\)	\(\overline{A}\)	\(\sum\)
\(I\)	0,0055	0,035	0,0405
\(\overline{I}\)	0,0495	0,91	0,9595
\(\sum\)	0,055	0,945	1

Erläuterung der Lösung

Aufgabenstellung

Übertrage die Vierfeldertafel auf dein Blatt und vervollständige diese.
(zur Kontrolle: \(P(A\cap I)=0,0055\))

Lösung

	\(A\)	\(\overline{A}\)	\(\sum\)
\(I\)	0,0055₃	0,035₆	0,0405₅
\(\overline{I}\)	0,0495₂	0,91	0,9595₄
\(\sum\)	0,055₁	0,945₇	1

Schwarz: Angabe direkt aus dem Text: \(P(A)=0,055\)

Rot: „Von diesen haben 90% keine Irritation“: \(\color{red}{P_A (\overline{I})=0,9}\)
Pfadregel: \(\color{red}{P(A\cap \overline{I})=P(A)\cdot P_A (\overline{I})=0,055\cdot 0,9= 0,0495} \)

Grün: Berechnung mittels Summenregel („Oben plus Mitte ist gleich unten“, „Links plus Mitte ist gleich rechts“)

Die Indizes geben die Reihenfolge der Bestimmung der Einträge wieder.

Teilaufgabe d)

Erwartungshorizont(offiziell)

Es ist \(P(A\cap I)=0,0055\).
Mit \(P(A)\cdot P(I)=0,055\cdot 0,0405=0,0022\neq 0,0055\) folgt die stochastische Abhängigkeit.

Erläuterung der Lösung

Aufgabenstellung

Zeige, dass das Auftreten der beiden Unverträglichkeiten stochastisch abhängig voneinander ist.

Lösung
Die stochastische (Un)abhängigkeit lässt sich überprüfen durch den Vergleich der Wahrscheinlichkeit der Schnittmenge mit dem Produkt der einzelnen Wahrscheinlichkeiten:
Wenn \(P(A\cap I)=P(A)\cdot P(I)\), dann wären beide Merkmale unabhängig voneinander (siehe Merkhilfe).
Es ist \(P(A\cap I)=0,0055\).
\(P(A)\cdot P(I)=0,055\cdot 0,0405=0,0022\neq 0,0055\)
Da \(P(A\cap I)\neq P(A)\cdot P(I)\), folgt die stochastische Abhängigkeit.

Teilaufgabe e)

Erwartungshorizont(offiziell)

\(P((A\cap \overline{I})\cup (\overline{A} \cap I))=0,0495+0,035=0,0845\).

Erläuterung der Lösung

Aufgabenstellung

Berechne die Wahrscheinlichkeit, dass entweder eine Allergie oder eine Irritation auftritt.

Lösung
Die Formulierung „entweder … oder …“ ist nicht zu verwechseln mit dem einfachen „oder“, bei dem der Additionssatz angewendet werden kann. Während beim Additionssatz die Schnittmenge \(A\cap I\) einmal mitgezählt wird (und ihre Wahrscheinlichkeit einmal abgezogen wird, damit sie nicht fälschlicherweise doppelt gezählt wird), kommt die Schnittmenge \(A\cap I\) bei „entweder … oder …“ überhaupt nicht vor.
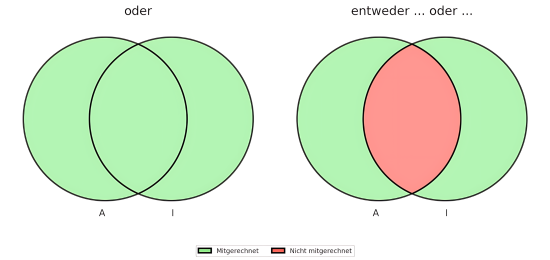
Venndiagramm_e).png

Gesucht ist die Wahrscheinlichkeit, dass eine Allergie, aber keine Irritation auftritt, addiert zur Wahrscheinlichkeit, dass eine Irritation, aber keine Allergie auftritt.
\(P((A\cap \overline{I})\cup (\overline{A} \cap I))=P(A\cap \overline{I})+ P(\overline{A} \cap I))=0,0495+0,035=0,0845\)

Teilaufgabe f)

Erwartungshorizont(offiziell)

\(A\): Allergie; \(I\): Irritation
\(P_I (A)=\frac{P(A\cap I)}{P(I)}= \frac{0,0055}{0,0405}\approx 0,136\)

Erläuterung der Lösung

Aufgabenstellung

Nachdem eine Testperson das Pflegeprodukt anwendet, tritt bei ihr eine Irritation auf. Ermittle, mit welcher Wahrscheinlichkeit sie auch allergisch reagiert.

Lösung
\(A\): Allergie; \(I\): Irritation
Die Irritation ist schon aufgetreten; sie ist also die Bedingung.
\(P_I (A)=\frac{P(A\cap I)}{P(I)}= \frac{0,0055}{0,0405}\approx 0,136\)

Teilaufgabe g)

Erwartungshorizont(offiziell)

Zufallsvariable \(G\): Gewinn bzw. Verlust für das Unternehmen
\(a\): Anteil aller Kunden, die eine Rückerstattung aus sonstigen Gründen beantragen

	keine Rückgabe	Rückgabe aufgrund von Unverträglichkeit	Rückgabe aus sonstigen Gründen
\(G_i\)	\(9\)	\(-0,5\)	\(-0,5\)
\(P(G=G_i)\)	\(0,91 -a\)	\(0,09\)	\(a\)

\(\mu=6,50\)
\(9\cdot (0,91-a)-0,5\cdot a-0,5\cdot 0,09=6,5 \ \implies \ a \approx 0,173\)
Es dürfen höchstens etwa 17,3% der Kunden aus sonstigen Gründen die Rückerstattung beantragen, damit das Unternehmen sein Ziel erreicht.

Erläuterung der Lösung

Aufgabenstellung

Das Unternehmen möchte einen durchschnittlichen Gewinn von mindestens 6,50€ pro Stück erwirtschaften.
Berechne, wie groß der Anteil aller Kunden höchstens sein darf, welche die Rückerstattung aus sonstigen Gründen beantragen.

Lösung
Zufallsvariable \(G\): Gewinn bzw. Verlust für das Unternehmen
\(a\): Anteil aller Kunden, die eine Rückerstattung aus sonstigen Gründen beantragen

	keine Rückgabe	Rückgabe aufgrund von Unverträglichkeit	Rückgabe aus sonstigen Gründen
\(G_i\)	\(9\)	\(-0,5\)	\(-0,5\)
\(P(G=G_i)\)	\(0,91 -a\)	\(0,09\)	\(a\)

Der erwartete Gewinn soll 6,50 € sein. Aus der Formel für den Erwartungswert (siehe Merkhilfe) ergibt sich eine Gleichung für \(a\).
\(\mu =\sum\limits_{i=1}^n P(X=x_i)\cdot x_i =P(X=x_1 )\cdot x_1+P(X=x_2 )\cdot x_2+\dots+P(X=x_n )\cdot x_n\)
\(\mu=(0,91-a)\cdot 9+ 0,09\cdot (-0,5) + a \cdot (-0,5)\)
\(\mu=6,50\)
\((0,91-a)\cdot 9- 0,09\cdot 0,5 -0,5a=6,5\)
Diese Gleichung kann nach dem gesuchten Wert für \(a\) aufgelöst werden.
\((0,91-a)\cdot 9-0,09\cdot 0,5-0,5a=6,5 \ \Leftrightarrow \ a\approx 0,173\)
Es dürfen höchstens etwa 17,3% der Kunden aus sonstigen Gründen die Rückerstattung beantragen, damit das Unternehmen sein Ziel erreicht.