Lösung Gleichungen grafisch lösen

a) \(D_f = ]-\infty; 1]\), \(W_f = \mathbb{R}_+\) und \(D_g = [-5; \infty[\), \(W_g = ]-\infty;3]\)
b)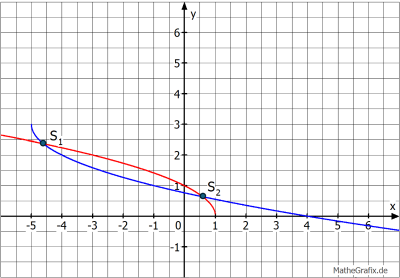

c)
Sei \(f(x)=\sqrt{-x+1}\) und \(g(x)=-\sqrt{x+5}+3\). Das Schaubild von \(f\) sei \(K_f\), das Schaubild von \(g\) sei \(K_g\). Man liest in der Zeichnung die x-Werte an den Stellen ab, an denen sich die Funktionsgraphen \(K_f\) und \(K_g\) schneiden. Diese x-Werte sind dann die Lösungen der gegebenen Wurzelgleichung.

d)
\(\sqrt{-x+1}=-\sqrt{x+5}+3\)
\(-x+1=x+5-2\cdot 3\cdot\sqrt{x+5}+9\) 
\(-2x-13=-6\sqrt{x+5}\)
\((-2x-13)^2=36(x+5)\) 
\(4x^2+52x+169=36x+180\)
\(4x^2+16x-11=0\) 
\(x_{1,2}=\frac{-16\pm\sqrt{16^2-4\cdot4\cdot(-11)}}{8}\)
\(x_{1,2}=\frac{-16\pm\sqrt{432}}{8}\) 
\(x_{1,2}=-2\pm\frac{3}{2}\sqrt{3}\) 

\(x_1=-2-\frac{3}{2}\sqrt{3}\) 
\(x_2=-2+\frac{3}{2}\sqrt{3}\) 

Die beiden Funktionsgraphen \(K_f\) und \(K_g\) schneiden sich an den Stellen \(x_1=-2-\frac{3}{2}\sqrt{3}\) und \(x_2=-2+\frac{3}{2}\sqrt{3}\).