Lösung Weg zur Schule

Version 22.1 von Dirk Tebbe am 2024/11/14 15:36

t [min]	1	2	5	10	15
v [m/s]	16,6	8,33	3,33	1,66	1,11

Bestimmen der Definitionslücke:
Die Definitionslücke tritt bei \( v = 0 \) auf, da eine Division durch Null nicht definiert ist. In diesem Kontext bedeutet \( v = 0 \), dass der Schüler eine Geschwindigkeit von 0 km/min hat, also nicht läuft.
Erläuterung der Definitionslücke:
Die Definitionslücke bei \( v = 0 \) ist sinnvoll, weil es unmöglich ist, eine Zeit zu berechnen, wenn der Schüler überhaupt nicht läuft. Eine Geschwindigkeit von 0 km/min bedeutet, dass der Schüler stillsteht, und daher wäre die benötigte Zeit unendlich.
Zeichnen des Graphen und Markieren der Definitionslücke:
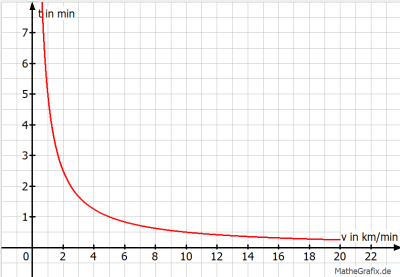
Hier ist eine Beschreibung, wie du den Graphen zeichnen kannst:
1) Zeichne eine horizontale v-Achse (Geschwindigkeit in km/h) und eine vertikale t-Achse (Zeit in Minuten).
2) Trage die Funktion \( t(v) = \frac{5}{v}\) für positive Werte von \( v \) ein.
3) Markiere die Definitionslücke bei \( v = 0 \) durch eine gestrichelte Linie oder eine andere Kennzeichnung.