Lösung Winkel am Einheitskreis
Zuletzt geändert von akukin am 2025/08/14 16:28
| Winkel \(\alpha\) | 30° | 60° | 90° | 120° | 150° | 180° | 210° | 240° | 270° | 300° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(\sin(\alpha)\) | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(1\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{2}\) | \(0\) | \(-\frac{1}{2}\) | \(-\frac{\sqrt{3}}{2}\) | \(-1\) | \(-\frac{\sqrt{3}}{2}\) | \(-\frac{1}{2}\) | \(0\) |
| \(\cos(\alpha)\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{2}\) | \(0\) | \(-\frac{1}{2}\) | \(-\frac{\sqrt{3}}{2}\) | \(-1\) | \(-\frac{\sqrt{3}}{2}\) | \(-\frac{1}{2}\) | \(0\) | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(1\) |
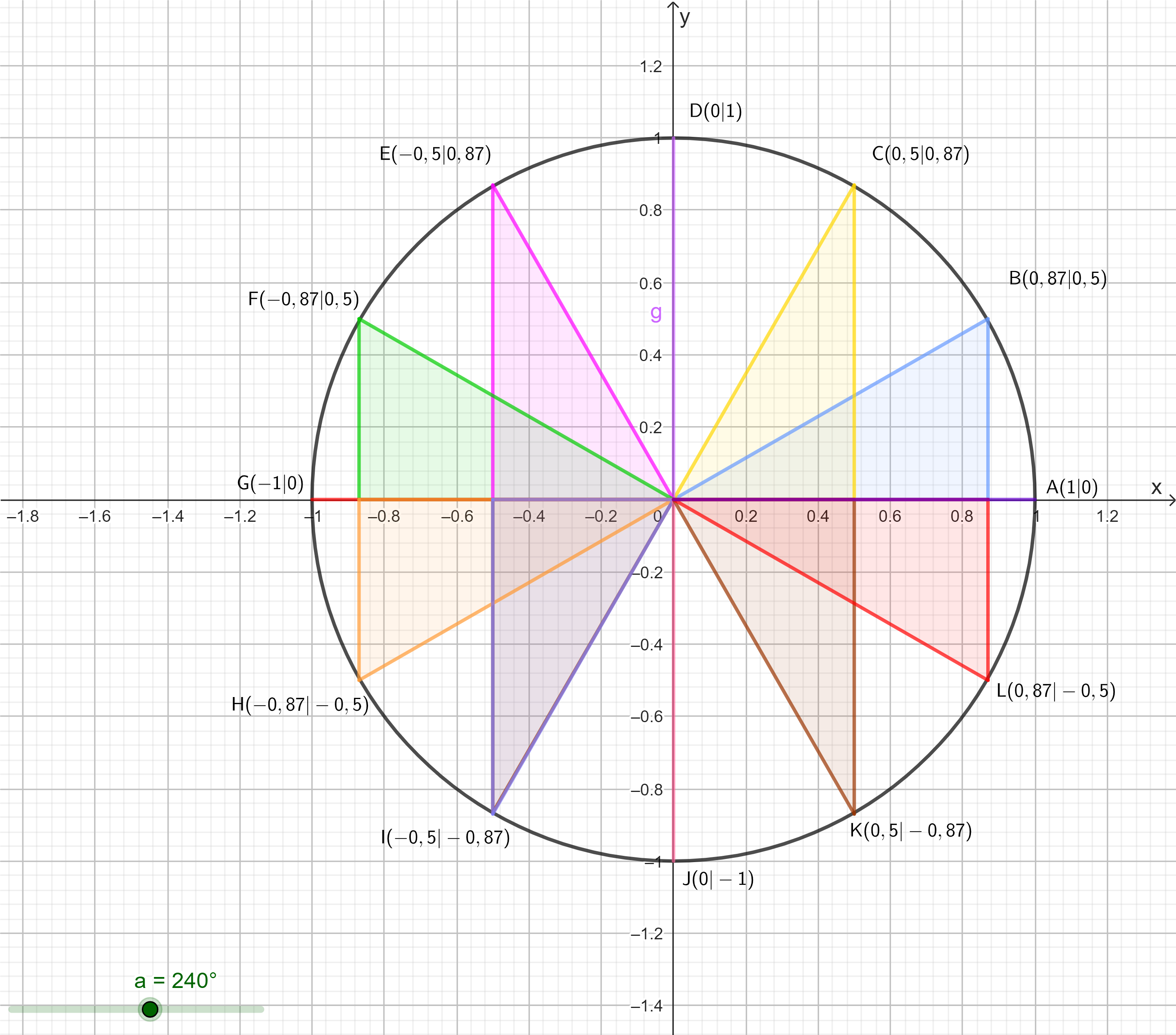
zu 2.
\(\sin(360 + \beta) = \sin(\beta)\) bzw. \(\cos(360 + \beta)=\cos(\beta)\)
