1.
\[\begin{align*}
\lim_{t\to 0}{h\left(2+t\right)}&=\lim_{t\to 0}{\left(20\cdot\sin{\left(2+t-2\right)}+20\cdot\sin{\left(2\right)}\right)} \\
&=\lim_{t\to 0}{\left(20\cdot\sin{\left(t\right)}+20\cdot\sin{\left(2\right)}\right)}=20\cdot\sin{\left(2\right)}
\end{align*}\]
Also gilt: \(h\left(2\right)= \lim \limits_{t\to0} h\left(2+t\right)\) und damit hat der Graph von h keinen Sprung, d.h. er ist stetig bei \(x=2\).
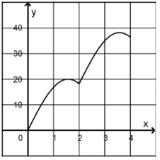
- Aus dem Graphen aus Teilaufgabe 1. ist ersichtlich, dass die Hochstelle im Intervall \(\left[3;4\right]\) liegt.
\(h\left(x\right)=20\cdot\sin{\left(x-2\right)}+20\cdot\sin{\left(2\right)} \ \text{für} \ 2<x\le4 \)
\(h^\prime\left(x\right)=20\cdot\cos{\left(x-2\right)}=0\ \ \Leftrightarrow\ \ x=\frac{\pi}{2}+2\approx3,5708\)
Nach ca. 3,6 Sekunden ist der Weckton am lautesten.
\[\begin{align*}
\bar{m}&=\frac{1}{b-a}\cdot\int_{a}^{b}{h\left(x\right)\mathrm{d} x} \\
&=\frac{1}{4}\cdot\int_{0}^{4}{h\left(x\right)\mathrm{d} x}=\frac{1}{4}\cdot\int_{0}^{2}{20\cdot\sin{\left(x\right)}\mathrm{d} x}+\frac{1}{4}\cdot\int_{2}^{4}{\left(20\cdot\sin{\left(x-2\right)}+20\cdot\sin{\left(2\right)}\right)\mathrm{d} x} \\
&=5\cdot\left[-\cos{\left(x\right)}\right]_0^2+5\cdot\left[-\cos{\left(x-2\right)}+\sin{\left(2\right)}\cdot x\right]_2^4 \\
&=-10\cdot\cos{\left(2\right)}+10+10\cdot\sin{\left(2\right)}\approx23,25
\end{align*}\]
Der durchschnittliche Funktionswert von h ist ca. 23.
