Hinweise und Lösungshilfen
Hinweis Teilaufgabe a)
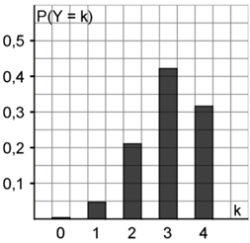
Bei der Zufallsgröße wird als Treffer gezählt, was bei der Zufallsgröße
den Nicht-Treffer darstellt und umgekehrt.
Folglich können Symmetrieeigenschaften verwendet werden, um die Wahrscheinlichkeitsverteilung von zu zeichnen.
Hinweis Teilaufgabe b)
Damit die Wahrscheinlichkeitsverteilungen der beiden binomialverteilten Zufallsgrößen und
identisch sein können, müssen die Parameter
und
gleich sein.
Hinweis Teilaufgabe c)
Der Parameter ist bei beiden Zufallsgrößen bereits gleich.
Wie kann formuliert werden, damit auch die Trefferwahrscheinlichkeiten
identisch sind?
Lösung:
Erläuterung:
Bei der Zufallsgröße Y wird als Treffer gezählt, was bei der Zufallsgröße X als Nicht-Treffer gezählt wird und umgekehrt.
Es gilt also: P(Y=0)=P(X=4); P(Y=1)=P(X=3); P(Y=2)=P(X=2) usw.
Folglich kann die Wahrscheinlichkeitsverteilung von X an der vertikalen Geraden durch k=2 gespiegelt werden, um die Wahrscheinlichkeitsverteilung von Y zu erhalten.