K4 K5 Ich kann die gegenseitige Lage von Parabeln und Geraden bestimmen.
K5 Ich kann gemeinsame Punkte von Parabeln und Geraden berechnen.
1 Lösung einer Schnittpunktberechnung überprüfen (k.A.)
Ein Schüler einer Eingangsklasse hat die gegenseitige Lage einer Parabel p und einer Geraden g bestimmt. Überprüfe sein Ergebnis.
\[\begin{align*}
-2x^2 + 6x - 3 &= -6x + 15 &&| +6x \\
-2x^2 + 12x - 3 &= 15 &&| -15 \\
-2x^2 + 12x - 18 &= 0 &&| :(-2) \\
x^2 - 6x + 9 &= 0
\end{align*}\]
\[x_{1/2} = \frac{6}{2} \pm \sqrt{\left(\frac{6}{2}\right)^2 - 9} \ \Rightarrow \text{Die Gerade } g \text{ ist eine Passante zur Parabel } p.\]
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB II - k.A. | Quelle Team Mathebrücke | #mathebrücke |
2 Parabeln finden (k.A.) 𝕃
Gesucht sind Parabeln, die durch den Punkt P gehen und die gegebene Gerade schneiden, berühren oder keinen Punkt mit ihr gemeinsam haben.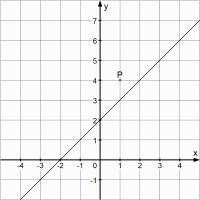
- Beschreibe deine Vorgehensweise.
- Wie viele Parabeln gibt es in jedem der drei Fälle?
- Bestimme für jeden Fall eine Gleichung einer Parabel. Schildere, wie du deine Ergebnisse überprüfen kannst.
- Hugo behauptet, der Scheitel einer berührenden Parabel läge auf der Geraden. Nimm dazu Stellung!
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB III - k.A. | Quelle Team Mathebrücke | #mathebrücke |
3 Gegenseitige Lage von Parabel und Gerade (k.A.) 𝕃
Überprüfe folgende Aussage:
Eine nach unten geöffnete Normalparabel mit dem Scheitel \(S(1|1)\) hat mit der Geraden \(g: y = x + 1\) einen gemeinsamen Schnittpunkt.
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB III - k.A. | Quelle Team Mathebrücke | #mathebrücke |
