Lösung Mandala berechnen

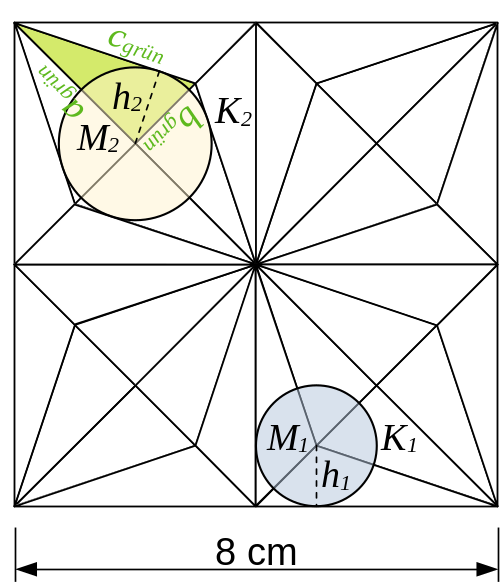
Es gilt \(a^2 + b^2 =4^2 + 4^2 = 32= c^2 \).
\( c= \sqrt{32}, A= c^2 = \sqrt{32} \cdot \sqrt{32} = 32 \)

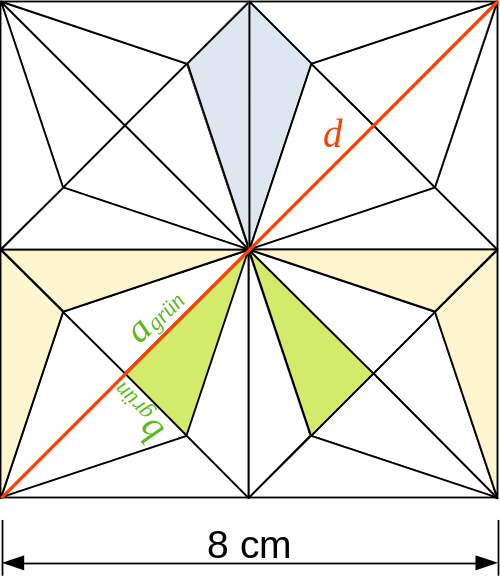
Feststellung: gelbe Dreiecke = blaue Dreiecke. Mit Hilfe der Strahlensätze erkennt man, dass die Höhe eines gelben Dreiecks \(\frac{1}{8}\) der Kantenlänge des Quadrats ist. Somit ist die Höhe 1 cm. Die Grundseite ist \(\frac{8}{2}=4cm\) lang.

\(\begin{align*} A_\Delta = \frac{1}{2} \cdot g \cdot h\\ A_\Delta = \frac{1}{2} \cdot 4 \cdot 1 =2\\ \end{align*}\)
6 Dreiecke: \(2 \cdot 6= 12cm^2\)
Berechnung er grünen Dreiecke:

1. Berechne die Diagonale des gesamten Quadrats und teile durch 4:
   \(\begin{align*} 8^2 +8^2 = 128\\ d= \sqrt{128} \\ a_{grün}= \frac{\sqrt{128}}{4}\\ \end{align*}\)
2. Berechne Seite \(b_{grün}:\)
   \(\begin{align*} b_{grün}= \frac{\sqrt{128}}{4}:2=\sqrt{2} \\ \end{align*}\)
3. Berechne die Fläche
   \(\begin{align*} A_{\Delta_{grün}}= \frac{1}{2} \cdot \sqrt{2} \cdot \frac{\sqrt{128}}{4} =2 \\ \end{align*}\)
4. Berechne den gesamten Flächeninhalt aller Flächen:
   \(\begin{align*} 2 \cdot A_{\Delta_{grün}} +12 = 2 \cdot 2 +12 =16 \\ \end{align*}\)
   Die Flächen haben einen gemeinsamen Flächeninhalt von \(16 cm^2\).