Lösung Rechteck im Graphen

Zuletzt geändert von akukin am 2024/10/13 20:22

Erwartungshorizont

$f^\prime\left(x\right)=3x^2-4ax+a^2$
Die Steigung von h beträgt
$-\frac{1}{f^\prime\left(0\right)}=-\frac{1}{a^2}$
so dass

durch den Term
$h\left(x\right)=-\frac{1}{a^2}x$
beschrieben wird. Flächeninhalt des Rechtecks:
$\left|h\left(a\right)\right|\cdot a=\frac{1}{a}\cdot a=1$

Erläuterung der Lösung

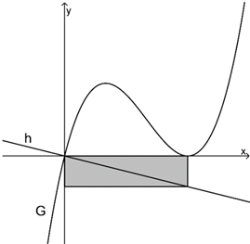
Das Rechteck geht vom Ursprung nach rechts bis zur zweiten Nullstelle (Berührstelle) von G und von dort nach unten bis zur Geraden

, da die Diagonale des Rechtecks auf

liegen soll.

Die Breite des Rechtecks ist der Abstand der beiden Nullstellen von

:
$f\left(x\right)=0$
$x^3-2ax^2+a^2x=0\ \ \Leftrightarrow\ \ x\left(x^2-2ax+a^2\right)=0$
Zweite Binomische Formel:
$x\left(x-a\right)^2=0$
Satz vom Nullprodukt:
$x=0 \ \vee \ x=a$
Die Breite des Rechtecks ist folglich $\left|a\right|$ (Betrag von

, da

auch negativ sein kann, die Breite des Rechtecks jedoch nicht.)

Für die noch fehlende Höhe des Rechtecks benötigen wir die Gleichung von

:
$f^\prime\left(x\right)=3x^2-4ax+a^2$
Steigung der Tangente an G im Ursprung: $f^\prime\left(0\right)=a^2$
Da die Gerade

senkrecht auf dieser Tangente steht, ist die Steigung von

: $m=-\frac{1}{f^\prime\left(0\right)}=-\frac{1}{a^2}$
Da

eine Ursprungsgerade ist, lautet ihre Gleichung:
$h\left(x\right)=-\frac{1}{a^2}x$
Um die Höhe des Rechtecks zu berechnen, setzen wir die zweite Nullstelle x=a

in die Gleichung von

ein: $h\left(a\right)=-\frac{1}{a^2}a=-\frac{1}{a}$
Die Höhe ist folglich $\left|-\frac{1}{a}\right|$
Der Flächeninhalt ergibt sich also zu $\left|a\right|\cdot\left|-\frac{1}{a}\right|=a\cdot\frac{1}{a}=1$ was unabhängig von

ist (was zu beweisen war).