BPE 2.2 Transformationen
Kompetenzen
K1 K4 Ich kann anhand von Funktionstermen beschreiben, wie ein Graph mittels Transformationen – unter Berücksichtigung der Reihenfolge – aus dem Graphen der unten aufgeführten Funktionen entsteht
K1 K4 Ich kann anhand von Funktionsgraphen beschreiben, wie ein Graph mittels Transformationen – unter Berücksichtigung der Reihenfolge – aus dem Graphen der unten aufgeführten Funktionen entsteht
K4 Ich kann zu einer verbal gegebenen Transformation den zugehörigen Funktionsterm angeben
K4 Ich kann zu einer grafisch gegebenen Transformation den zugehörigen Funktionsterm angeben
\(f(x) = x^2\), \(f(x) = \frac{1}{x}\), \(f(x) = \sqrt{x}\)
1 Terme bestimmen (6 min) 𝕀 𝕃
Die Funktionen \(f, g\) und \( h\) sind transformierte Potenzfunktionen mit den Graphen Kf, Kg und Kh. Bestimme die jeweiligen Funktionsterme.
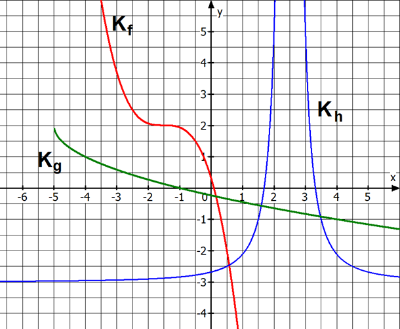
| AFB I - K4 | Quelle k.A. |
2 Potenzfunktionen verschieben (8 min) 𝕃
Die Funktionen \(f, g\) und \( h\) sind transformierte Potenzfunktionen mit den zugehörigen Graphen Kf, Kg und Kh. Beschreibe die jeweils vorgenommene Transformation.
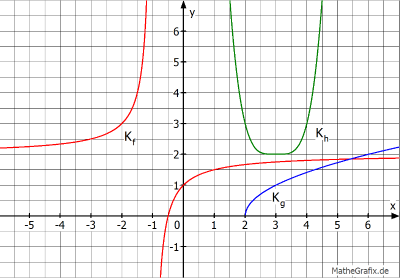
| AFB II - K1 K4 | Quelle Niklas Wunder |
3 Transformationen (8 min) 𝕃
Die Schaubilder der Funktionen in der obersten Reihe sollen durch die folgenden Transformationen verändert werden. Ermittle die fehlenden Gleichungen bzw. Transformationen in der Tabelle.
| Transformation | \(y = x^2\) | \(y = x^3\) | \(y = x^{-1} = \frac{1}{x}\) | \(y = x^\frac{1}{2} = \sqrt{x}\) |
| Verschiebung um 1 nach oben | \(y = x^2 + 1\) | |||
| \(y = x^2 - 2\) | \(y = x^3 - 2\) | \(y = x^{-1} - 2 = \frac{1}{x} - 2\) | ||
| Vertikale Streckung mit Faktor 0,8 | ||||
| Verschiebung um 1,5 nach rechts | ||||
| \(y = (x + 2,5)^2\) | ||||
| \(y = -x^2\) |
| AFB I - K5 K6 | Quelle Martina Wagner |
4 Transformationen verstehen (15 min) 𝕋 𝕃
Gegeben sind Wertetabellen von Parabeln. Beschreibe jeweils, wie aus den x-Werten die y-Werte entstehen und gib die Gleichung der Parabel an.
Beispiel
| x-Werte | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y-Werte | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 |
Beschreibung: x-Werte → quadrieren → y-Werte
Gleichung: y = x2
x-Werte -4 -3 -2 -1 0 1 2 3 4 y-Werte 19 12 7 4 0 4 7 12 19 Beschreibung: x-Werte → quadrieren → ? → y-Werte
Gleichung:x-Werte -4 -3 -2 -1 0 1 2 3 4 y-Werte 36 25 16 9 4 1 0 1 4 Beschreibung: x-Werte → ? → ? → y-Werte
Gleichung:x-Werte -4 -3 -2 -1 0 1 2 3 4 y-Werte 48 27 12 3 0 3 12 27 48 Beschreibung: x-Werte → ? → ? → y-Werte
Gleichung:x-Werte -4 -3 -2 -1 0 1 2 3 4 y-Werte 9 4 1 0 1 4 9 16 25 Beschreibung: x-Werte → ? → ? → y-Werte
Gleichung:
| AFB II - K4 K5 K6 | Quelle Martina Wagner |
5 Transformationen von Funktionsgraphen beschreiben (6 min) 𝕃
Beschreibe, wie die Schaubilder der nachfolgenden Funktionen jeweils aus dem Graphen \( y=x^k; k \in \mathbb{Q} \) entstanden sind.
- \(g(x)=6x^4-1\)
- \(g(x)=-\frac{1}{2}(x-5)^4-3\)
- \(g(x)=\frac{1}{(x+3)^2}-8\)
- \(g(x)=-4\,\sqrt[3]{x+1}+5\)
| AFB I - K1 K4 | Quelle Martin Stern |
6 Funktionsterme nach Transformationen bestimmen (8 min) 𝕃
Gegeben ist die Funktion \(f\) mit \(f(x)=\frac{1}{x}\). Bestimme die Funktionsgleichung der Funktion \(g\).
- Der Graph von \(g\) entsteht aus dem Graphen von \(f\) durch Spiegelung an der x-Achse, Streckung mit dem Faktor 2 in y-Richtung, Verschiebung um 1 in x-Richtung und Verschiebung um 3 in y-Richtung.
- Der Graph von \(g\) entsteht aus dem Graphen von \(f\) durch Verschiebung um 1 in x-Richtung, Verschiebung um 3 in y-Richtung, Streckung mit dem Faktor 2 in y-Richtung und Spiegelung an der x-Achse.
- Der Graph von \(g\) entsteht aus dem Graphen von \(f\) durch Verschiebung um 1 in x-Richtung, Streckung mit dem Faktor 2 in y-Richtung, Verschiebung um 3 in y-Richtung und Spiegelung an der y-Achse.
| AFB II - K4 | Quelle Martin Stern, Martin Rathgeb |
Inhalt für Lehrende (Anmeldung erforderlich)
