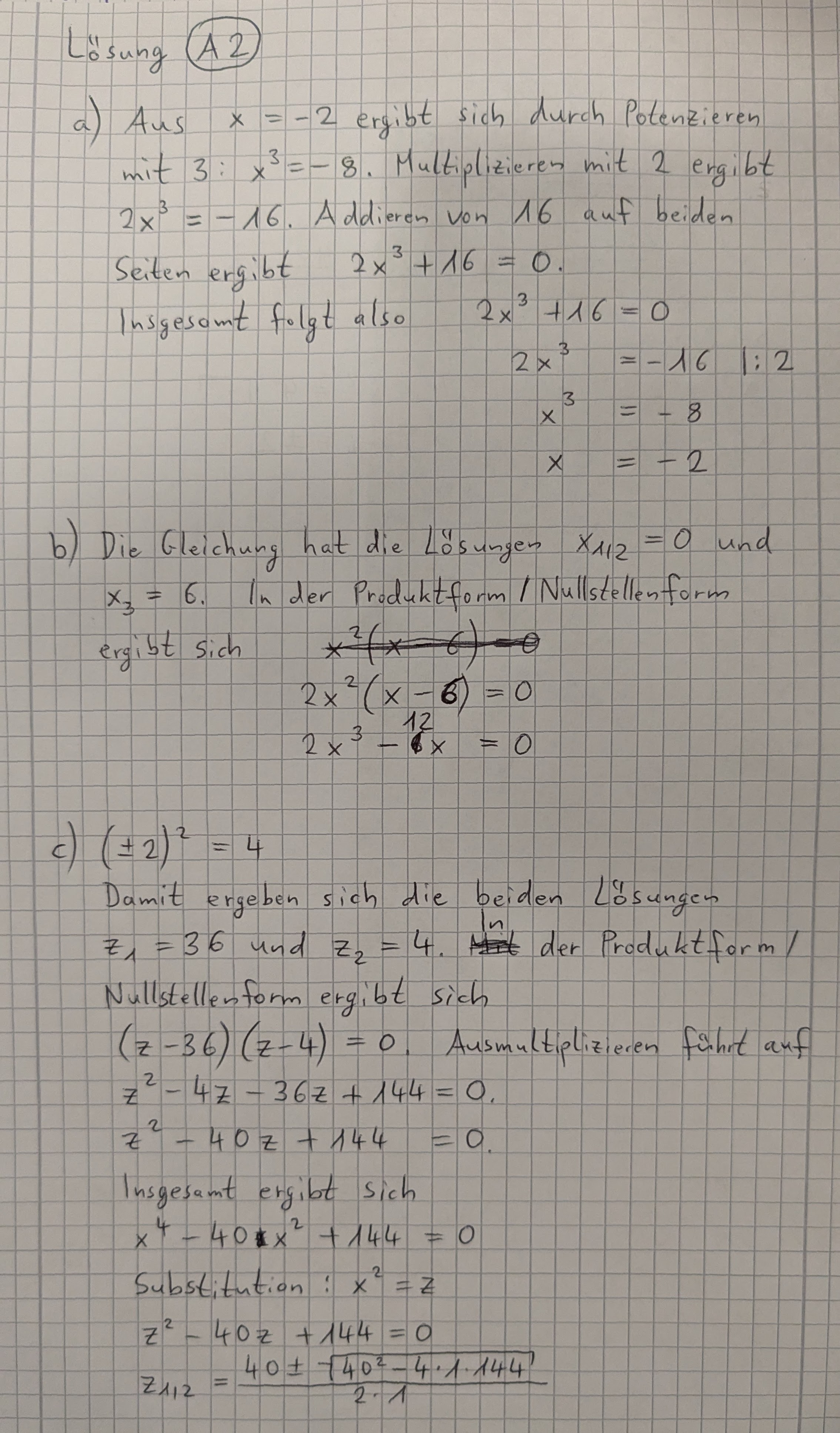a) Aus \(x=-2\) ergibt sich durch Potenzieren mit \(3\): \(x^3=-8\)
Multiplizieren mit \(2\) ergibt \(2x^3=-16\)
Addieren von \(16\) auf beiden Seiten ergibt \(2x^3+16=0\)
Insgesamt folgt also:
\[\begin{align}
2x^3+16&=0 \\
2x^3&=-16 \quad \mid :2 \\
x^3&=-8 \\
x&=-2
\end{align}\]
b) Die Gleichung hat die Lösungen \(x_{1,2}=0\) und \(x_3=6\). In der Produktform/Nullstellenform ergibt sich:
\[\begin{align}
2x^3(x-6)=0 \\
2x^3-12x^2=0
\end{align}\]
c) \((\pm 2)^2=4\)
Damit ergeben sich die beiden Lösungen \(z_1=36\) und \(z_2=4\). In der Produktform/Nullstellenform ergibt sich \((z-36)(z-4)=0\). Ausmultiplizieren führt auf \(z^2-4z-36z+144=0\)
\[\begin{align}
z^2-4z-36z+144=0 \\
\Leftrightarrow z^2-40z+144=0
\end{align}\]
Insgesamt ergibt sich \(x^4-40x^2+144=0\)
\[\begin{align*}
x^4-40x^2+144 &= 0 & \left|\left|\text{ Subst.: } & x^2:=z\\
z^2-40z+144=0 &= 0 & \left|\left|\text{ SVNP } &
\end{align*}\]
\[\begin{align*}
\Rightarrowz_{1,2}&=\frac{\square\pm\sqrt{\square^2-4\cdot\square\cdot\square}}{2\cdot\square}\\
z_1&=\frac{\square+\square}{\square}; z_2=\frac{\square-\square}{\square}
\end{align*}\]
\[\begin{align*}
&\text{Resubst.: } \square := x^2\\
&x_{1,2}^2=36 \Rightarrow x_{1,2}=\square\\
&x_{3,4}^2=\square \Rightarrow x_{3,4}=\pm 2
\end{align*}\]