\(B(t)=-0,3t^3+9,3t^2-56,4t-66\)
1.\(B(10)=-0,3\cdot 10^3+9,3\cdot 10^2-56,4\cdot 10-66=0\)
\(B(22)=-0,3\cdot 22^3+9,3\cdot 22^2-56,4\cdot 22-66=0\)
1.3h vor Badeschluss bedeutet 19:00 Uhr: \(B(19)=-0,3\cdot 19^3+9,3\cdot 19^2-56,4\cdot 19-66=162\)
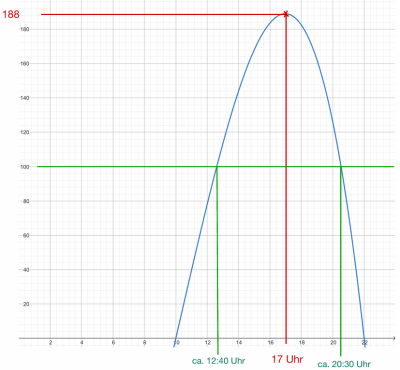
- Aus dem Graph kann man ablesen: um ca. 17:00 Uhr sind etwa 188 Besucher im Bad.
1.Der Zeitraum ist näherungsweise von 12:40 Uhr bis 20:30 Uhr.
1.Rechnerisch müsste man die Funktion \(B(t)\) mit der Geraden \(g(t)=100\) schneiden:\(B(t)=100\) und die Schnittpunkte mit einem geeigneten Lösungsverfahren berechnen.