Zum Inhalt springen

Lösung Bewegung

Version 6.1 von Holger Engels am 2025/07/15 08:53
  1. Das ist aufgrund des Schaubilds schwer zu sagen. Etwa im Intervall \([3,4;4,8]\) könnte \(\Delta y\) 0 und somit die mittlere Geschwindigkeit auch 0 sein. Es könnte sich auch um einen Sattelpunkt handeln. Das wäre ein Punkt, wo die Steigung exakt 0 ist, unmittelbar davor und danach wäre sie dann schon wieder leicht positiv. Dann gäbe es kein Intervall mit mittlerer Änderungsrate 0 sonder nur eine Stelle mit momentaner Änderungsrate 0.
  2. Die mittlere Geschwindigkeit im Intervall \([4;8]\) beträgt \(\frac{\Delta y}{\Delta t}=\frac{4-2}{8-4}=\frac{2}{4}=0,5 \frac{\text{m}}{\text{s}}\). Die Aussage ist somit wahr.
  3. Falsch. Legen wir eine Tangente an der Stelle \(t=8\) an (siehe Bild), so ergibt sich eine Steigung von etwa \(1,5 \frac{\text{m}}{\text{s}}\) für die Tangente, das heißt eine momentane Geschwindigkeit von \(1,5 \frac{\text{m}}{\text{s}}\).
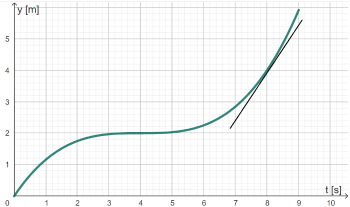
    GraphmitTangente.png
  4. Falsch. Wir wissen von Teilaufgabe c), dass die momentane Änderungsrate zum Zeitpunkt \(t=8\) \(1,5 \frac{\text{m}}{\text{s}}\) beträgt und somit größer ist als \(1 \frac{\text{m}}{\text{s}}\).
  5. Falsch. Da die Tangente an der Stelle \(t=0\) nicht waagerecht ist, ist die momentane Geschwindigkeit nicht \(0 \frac{\text{m}}{\text{s}}\).