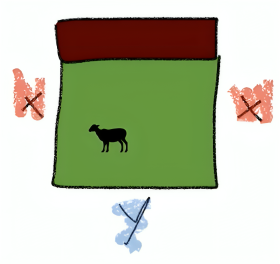
Hauptbedingung:
\(A= x \cdot y\)
Nebenbedingung:
\[\begin{align*}
2x+y &= 110 \quad \mid -2x\\
\Leftrightarrow y &= 110-2x \\
\end{align*}\]
Einsetzen von \(y= 110-2x\) in die Hauptbedingung liefert die Zielfunktion
\(A(x)=x\cdot (110-2x)=-2x^2+110x\)
mit \(A'(x)=-4x+110\)
Gleichsetzen der ersten Ableitung mit Null liefert
\[\begin{align*}
&\: A'(x) &\:= 0 \\
&\: \Leftrightarrow &\: -4x+110 &\: = 0 &\: \mid -110 \\
&\: \Leftrightarrow &\: -4x &\: \qquad =-110 &\: \mid :(-4) \\
&\: \Leftrightarrow &\: x &\: = 27,5
\end{align*}\]
Da \(A''(x)=-4 < 0\), liegt ein Maximum vor.
Es ist \(A(27,5)=1512,5 \text{m}^2\).
An den Rändern des Definitionsbereiches \(D=[0,110]\) gilt \(A(0)=0\) und \(A(110)=0\). Damit liegt bei \(x=27,5\) ein globales Maximum vor.
Einsetzen in die NB: \(y=100-2\cdot 27,5=55\).
Somit ist der Flächenhalt maximal für die Seitenlängen \(x=27,5 \text{m}\) und \(y=55 \text{m}\).
