BPE 2.2 Transformationen
Kompetenzen
K1 K4 Ich kann anhand von Funktionstermen beschreiben, wie ein Graph mittels Transformationen – unter Berücksichtigung der Reihenfolge – aus dem Graphen der unten aufgeführten Funktionen entsteht
K1 K4 Ich kann anhand von Funktionsgraphen beschreiben, wie ein Graph mittels Transformationen – unter Berücksichtigung der Reihenfolge – aus dem Graphen der unten aufgeführten Funktionen entsteht
K4 Ich kann zu einer verbal gegebenen Transformation den zugehörigen Funktionsterm angeben
K4 Ich kann zu einer grafisch gegebenen Transformation den zugehörigen Funktionsterm angeben
\(f(x) = x^2\)
\(f(x) = \frac{1}{x}\)
\(f(x) = \sqrt{x}\)
1 Terme bestimmen (k.A.) 𝕀 𝕃
Die Funktionen f, g und h sind verschobene Potenzfunktionen mit den zugehörigen Schaubildern Kf, Kg und Kh. Bestimmen Sie die jeweiligen Funktionsterme.
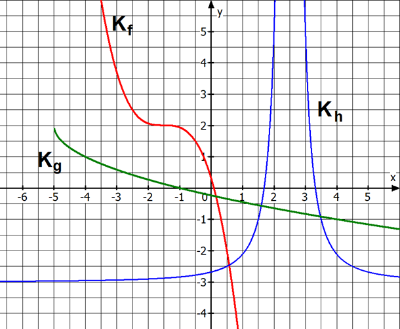
| AFB I - K4 | Quelle KMap |
2 Potenzfunktionen verschieben (8 min) 𝕃
Die Funktionen \(f, g\) und \( h\) sind verschobene Potenzfunktionen mit den zugehörigen Schaubildern Kf, Kg und Kh. Beschreibe wie die verschobenen Potenzfunktionen aus den ursprünglichen Funktionen hervorgehen.
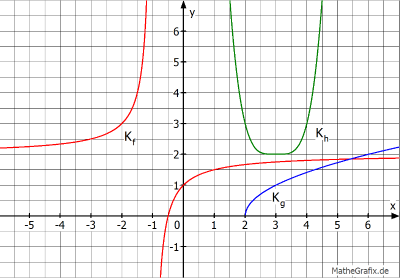
| AFB I - K1 K4 | Quelle Niklas Wunder |
3 Transformationen von Funktionsgraphen beschreiben (12 min) 𝕃
Beschreibe, wie die Schaubilder der nachfolgenden Funktionen jeweils aus dem Graphen \( y=x^k; k \in \mathbb{Q} \) entstanden sind.
a) \(f(x)=6x^4-1\)
b) \(f(x)=-\frac{1}{2}(x-5)^4-3\)
c) \( f(x)=\frac{1}{(x+3)^2}-8\)
d) \(f(x)=-4\,\sqrt[3]{x+1}+5\)
| AFB I - K1 K4 | Quelle Martin Stern |
4 Funktionsterme nach Transformationen bestimmen (5 min) 𝕃
Bestimme jeweils einen passenden Funktionsterm.
a) Der Graph von \(K_f\) entsteht aus dem Graphen \(f(x)=\frac{1}{x}\) durch Spiegelung an der x-Achse, Streckung mit dem Faktor \(\2\) in y-Richtung sowie durch Verschiebung um 1 nach rechts und um 3 nach oben.
b) Der Graph von \(K_f\) entsteht aus dem Graphen \(f(x)=\frac{1}{x}\) durch Verschiebung um 1 nach rechts, Streckung mit dem Faktor \(\2\) in y-Richtung, Spiegelung an der x-Achse und Verschiebung um 3 nach oben.
| AFB I - K4 | Quelle Martin Stern |
