Aufgabe 2 (Pyramide)

Gegeben ist eine Pyramide mit quadratischer Grundfläche. Gegeben sind die Punkte \(A(12|0|2), B(12|8|2), C(4|8|2)\) und \( S(8|4|7,5)\).

1. Zeichne die Pyramide in ein dreidimensionales Koordinatensystem und benenne den Eckpunkt D.
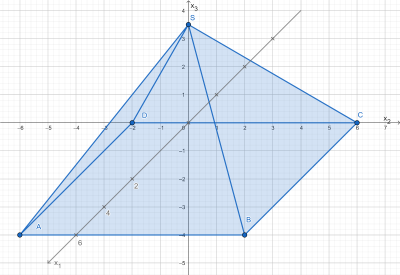   Siehe Grafik mit Punkt \(D(4|0|2)\)
2. Bestimme den Mittelpunkt M der Grundfläche der Pyramide.
   \(M(-8|4|2)\) mit \(\vec{M}= \frac{1}{2}(\vec{A}+\vec{C})\)
3. Zeige, dass es sich um eine quadratische Grundfläche handelt.
   \(\vec{AB}= \left(\begin{array}{c} 0 \\ 8 \\ 0 \end{array}\right)\), \(\vec{BC}= \left(\begin{array}{c} -8 \\ 0 \\ 0 \end{array}\right)\), \(\vec{CD}= \left(\begin{array}{c} 0 \\ -8 \\ 0 \end{array}\right)\), \(\vec{DA}= \left(\begin{array}{c} 8 \\ 0 \\ 0 \end{array}\right)\),
   \(\vec{AB}\cdot\vec{BC}= \left(\begin{array}{c} 0 \\ 8 \\ 0 \end{array}\right)\cdot \left(\begin{array}{c} -8 \\ 0 \\ 0 \end{array}\right)=0 \)
   und \(\vec{AB}=-\vec{CD}\)
   und \(\vec{BC}=-\vec{DA}\)
4. Erläutere die geometrische Bedeutung von \(\vec{MA}\cdot\vec{MS}=0\).
   Der Vektor \(\vec{MS}\) steht senkrecht auf dem Vektor \(\vec{MA}\). Somit steht die Höhe \(\vec{MS}\) senkrecht auf der Diagonalen \(\vec{AC}\)
5. Untersuche, welche besondere Lage die Grundfläche der Pyramide im Koordinatensystem hat.
   Die Grundfläche der Pyramide liegt parallel zur \(x_1x_2\) Ebene