Aufgabe 3 (Würfel)

Die Punkte \(A(0|0|0), B(5|0|0), C(5|5|0)\) und \(H(0|0|5)\) bilden die Eckpunkte eines Würfels.

1. Bestimme, die fehlenden Koordinaten der Punkte D, E und G des Würfels und skizziere diesen in ein dreidimensionales Koordinatensystem.
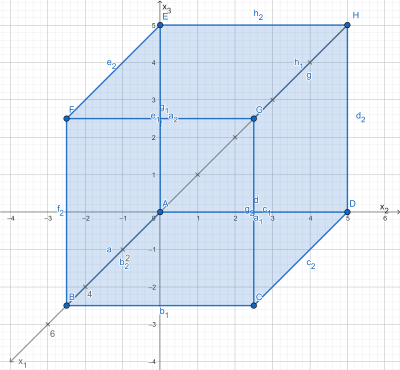   Siehe Graftik, es gilt:
   \( D(0|5|0)\), \( E(0|0|5)\), \( F(5|0|5)\), \( G(5|5|5)\), \( H(0|5|5)\).

1. Zeige, dass das Volumen des Würfels 125 Volumeneinheiten beträgt.
   \(\vec{AB}= \left(\begin{array}{c} 5 \\ 0 \\ 0 \end{array}\right)\), \(\vec{AD}= \left(\begin{array}{c} 0 \\ 5 \\ 0 \end{array}\right)\),
   \(\vec{AE}= \left(\begin{array}{c} 0 \\ 0 \\ 5 \end{array}\right)\), \(\left|\vec{AB}\right|=5\), \(\left|\vec{AD}\right|=5\), \(\left|\vec{AE}\right|=5\),
   Für das Volumen gilt \(V=5\cdot 5\cdot 5=125\)
2. Das Volumen einer Pyramide berechnet sich durch die Formel \(V=\frac{1}{3} \cdot G\cdot h\)
   Skizziere in ein dreidimensionales Koordinatensystem eine Pyramide mit dreieckiger Grundfläche, die das gleiche Volumen wie der Würfel besitzt. Gib die Eckpunkte deiner Pyramide an.
   Mit \(V=\frac{1}{3}\cdot G\cdot h\)
   Grundfläche Dreieck ABC mit \( A(0|0|0)\),\( B(5|0|0)\), \( D(0|5|0)\) daraus folgt \(G=\frac{1}{2}\cdot 5\cdot 5=12,5 FE\)
   \(V=\frac{1}{3} \cdot G\cdot h\)
   \(125=\frac{1}{3} \cdot 12,5\cdot h\)
   \(h= 30\)