Zum Inhalt springen

Tipp Aufgabe 1

Zuletzt geändert von akukin am 2024/12/28 16:52

Teilaufgabe a)

Hinweis Die Untersuchung des Funktionsterms einer Polynomfunktion lässt viele Schlüsse auf den Verlauf des Graphen zu, zum Beispiel auf sein globales und lokales Verhalten, aber auch auf seine eventuellen Symmetrieeigenschaften.

Teilaufgabe b)

Hinweis 1 An Extremstellen ist die erste Ableitung Null, da an Hoch- bzw. Tiefpunkten immer eine waagrechte Tangente angelegt werden kann.
Hinweis 2 Mit Hilfe der zweiten und gegebenenfalls dritten Ableitung lässt sich überprüfen, ob die Stellen, an denen die erste Ableitung Null ist, Hochstellen, Tiefstellen oder Sattelstellen sind.
Hinweis 3 Die y-Koordinate der Punkte erhält man, wenn man den jeweiligen x-Wert in den Funktionsterm einsetzt.

Teilaufgabe c)

Hinweis Dass x=2 eine Nullstelle ist, lässt sich am einfachsten überprüfen, indem man x=2 in den Funktionsterm einsetzt.

Teilaufgabe d)

Hinweis 1 Eine Skizze des Funktionsgraphen, der Wendepunkte und dazugehörigen Tangenten könnte helfen.
Hinweis 2 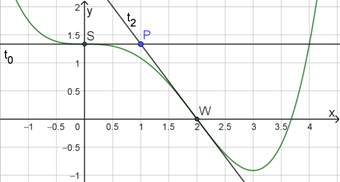1d)Hinweis2.png Die Tangentengleichungen können zum Beispiel mit Hilfe der allgemeinen Formel (siehe Merkhilfe) ermittelt werden.

Teilaufgabe e)

Hinweis 1 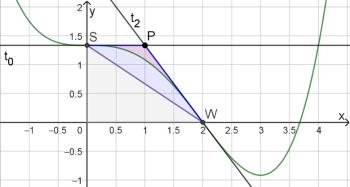1e)Hinweis.png Gesucht ist der Inhalt der roten Teilfläche.
Versuche, diesen mit Hilfe der Flächeninhalte der blauen und grauen Dreiecke sowie mit einem Integral auszudrücken.
Hinweis 2 1e)Hinweis.png Das blaue Dreieck PSW hat die Grundlinie SP und die Höhe SO (O ist der Ursprung des Koordinatensystems). Der Flächeninhalt des gesamten blauen Dreiecks PSW kann also mit Hilfe der Dreiecksformel aus der Mittelstufe (siehe Merkhilfe) berechnet werden.
Hinweis 3 1e)Hinweis.png Der Flächeninhalt des Teils des Dreiecks PSW, der unterhalb des Graphen von f liegt, ist das Integral von 0 bis 2 über die Funktion f, aber ohne den Flächeninhalt des grauen Dreiecks OWS.