Lösung Stochastik
Zuletzt geändert von akukin am 2026/01/25 18:16
Teilaufgabe a)
Erwartungshorizont
\(\mu = 6\)Erläuterung der Lösung
AufgabenstellungGib den Erwartungswert der Zufallsgröße \(X\) an.
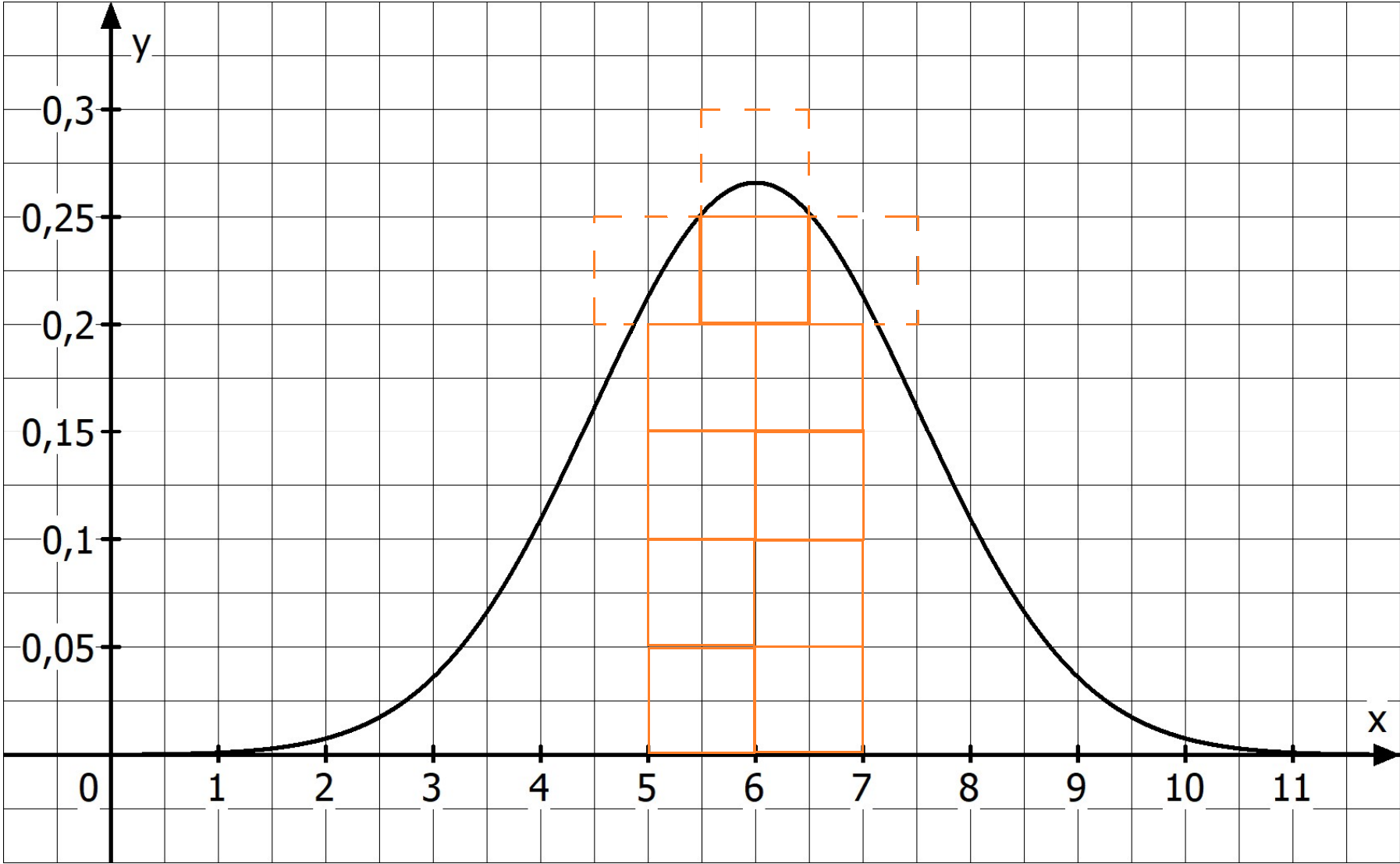
LösungDer Hochpunkt des Graphen liegt bei \(x=6\). Somit ist der Erwartungswert \(\mu = 6\).
Teilaufgabe b)
Erwartungshorizont
\(\sigma \approx 1{,}5\), da der Graph der Dichtefunktion Wendestellen bei \(x \approx 4{,}5\) und \(x \approx 7{,}5\)Erläuterung der Lösung
AufgabenstellungGib näherungsweise den Wert der Standardabweichung von \(X\) an. Begründe diesen.
LösungDer Graph der Dichtefunktion besitzt Wendestellen bei \(x_1 \approx 4{,}5\) und \(x_2\approx 7{,}5\).
Für die Wendestellen einer Normalverteilung gilt: \(x_{1,2}=\mu\pm\sigma\)
Die Standardabweichung beträgt somit ungefähr \(\sigma\approx 6-4{,}5=7{,}5-6=1,5\).
Teilaufgabe c)
Erwartungshorizont
Zum Beispiel durch Kästchenzählen (etwa 10 Kästchen mit jeweils 0,05 Flächeneinheiten) erhält man\(P(5\leq X\leq 7)\approx 10\cdot 0{,}05=0,5\)
Erläuterung der Lösung
AufgabenstellungErmittle näherungsweise die Wahrscheinlichkeit, dass der Wert der Zufallsgröße \(X\) im Intervall \([5;7]\) liegt.
LösungDie Wahrscheinlichkeit kannst du bestimmen, indem du durch Kästchenzählen die Fläche bestimmst, die im Intervall \([5;7]\) zwischen dem Graphen und der \(x\)-Achse eingeschlossen wird. Ein Quadrat mit jeweils zwei Kästchen Länge und Breite umschließt dabei eine Fläche von \(1\cdot 0{,}05\). Innerhalb des Intervalles zählen wir etwa 10 solcher Quadrate.
Das heißt, es gilt
\(P(5\leq X\leq 7)\approx 10\cdot 0{,}05=0,5\)