BPE 2.3 Potenzgleichungen
K5 Ich kann Lösungen einfacher Potenzgleichungen algebraisch bestimmen
K1 Ich kann die Notwendigkeit einer Probe beim Lösen einer Wurzelgleichung begründen
1 Einfache Gleichungen (4 min) 𝕃
Bestimmen Sie die Lösungen der Potenzgleichung.
a) \(x^8=256\)
b) \(x^3=-216\)
c) \(x^5=243\)
d) \(x^{10}=-1024\)
e) \(x^4=\frac{1}{81}\)
f) \(x^6+\frac{1}{6}=0\)
g) \(\frac{27}{216}=x^3\)
h) \(\frac{1}{81}=x^8\)
| AFB I - K5 | Quelle kickoff |
2 Kaffetasse (3 min) 𝕃
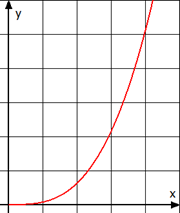 Die Abbildung zeigt den Querschnitt einer Kaffeetasse. Die Wanddicke der Tasse ist zu vernachlässigen. Der Kurvenbogen wird beschrieben durch das Schaubild Kf mit \(f(x)=\frac{1}{4} x^3 \), x ist der Tassenradius in cm, y die Tassenhöhe in cm.
Die Abbildung zeigt den Querschnitt einer Kaffeetasse. Die Wanddicke der Tasse ist zu vernachlässigen. Der Kurvenbogen wird beschrieben durch das Schaubild Kf mit \(f(x)=\frac{1}{4} x^3 \), x ist der Tassenradius in cm, y die Tassenhöhe in cm.
Die Tasse hat eine Höhe von 10 cm. Bestimme den Umfang des Tassenrandes.
| AFB II - K5 | Quelle kickoff |
3 Gleichungen finden (4 min) 𝕃
Ermitteln Sie jeweils eine Gleichung mit den folgenden Eigenschaften.
a) Gleichung vom Grad 4 und \(\mathbb{L} = \lbrace -4; 4 \rbrace\)
b) Gleichung vom Grad 5 und \(\mathbb{L} = \lbrace 5 \rbrace\)
| AFB II - K4 K2 K5 | Quelle Martina Wagner |
4 Probe Wurzelgleichungen (10 min) 𝕃
Löse die folgenden Wurzelgleichungen. Führe anschließend eine Probe der Lösungen durch um unpassende Lösungen auszusortieren.
a) \(\sqrt{x+4}=x-2\)
| AFB II - K5 | Quelle Niklas Wunder |
