Lösung Musterklassenarbeit Aufgabe 2

a) Da jede reelle Zahl in die Funktion eingesetzt werden kann, ist der maximale Definitionsbereich die Menge der reellen Zahlen, das heißt \( D = \mathbb{R} \).

Da die Funktion eine nach oben geöffnete Parabel ist, die um zwei nach oben verschoben wurde (siehe Abbildung), ist der Wertebereich \([2; \infty[\).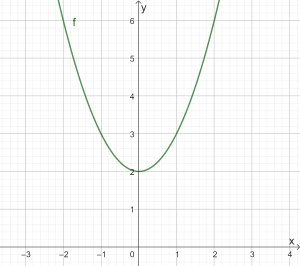

b) Die Funktion lässt sich als Bruch umschreiben zu \(f(x)=-(x-5)^{-2}=-\frac{1}{(x-5)^2}\). Man sieht so, dass an der Stelle \(x=5\) eine Definitionslücke vorliegt, da der Nenner an der Stelle 0 wäre („Man darf nicht durch 0 teilen“). Der maximale Definitionsbereich ist somit die Menge der reellen Zahlen ohne 5, d.h. \( D= \mathbb{R}\setminus \{5\}\).

Um ausgehend von dem Graphen der Funktion \(g(x)=\frac{1}{x^2}\) den Graphen der Funktion \(f(x)=-\frac{1}{(x-5)^2}\) zu erhalten, spiegelt man den Graphen von \(g(x)\) an der x-Achse und verschiebt ihn um 5 nach rechts, wodurch sich folgender Graph ergibt:

Die Wertemenge ist demnach die Menge der negativen reellen zahlen, das heißt \( W= ]-\infty;0[= \mathbb{R}^*_- \).
Alternativ erhält man die Wertemenge durch Einsetzen möglicher x-Werte des Definitionsbereiches. Man erkennt dabei, dass man nur negative y-Werte erhält, da der Nenner aufgrund des Quadrates für alle x-Werte immer größer als 0 ist und somit \(\frac{1}{(x-5)^2}\) auch immer größer als 0 ist. Wegen des negativen Vorzeichens ist somit \(f(x)=-\frac{1}{(x-5)^2}\) immer negativ.

c) Die Funktion lässt sich als Bruch umschreiben zu \(f(x)=x^{-3}=\frac{1}{x^3}\). Der einzige x-Wert, für den der Nenner 0 wird, ist  \(x=0\). Der maximale Definitionsbereich ist also \( D = \mathbb{R}\setminus \{0\}\).

Durch Ausprobieren erkennt man, dass der Funktionswert alle Zahlen außer 0 einnehmen kann.
Der Wertebereich ist also ebenso  \( W = \mathbb{R}\setminus \{0\}\).