BPE 12.2 Ableitungsfunktion und Ableiten
K4 Ich kann ausgehend vom grafischen Differenzieren, Ableitungen für ausgewählte Funktionen bestimmen
K1 K6 Ich kann die Bedeutung der Eulerschen Zahl e als besondere Basis bei Exponentialfunktionen zur Berechnung ihrer Ableitung nennen
K1 K6 Ich kann den Zusammenhang von trigonometrischen Funktionen mit ihren Ableitungsfunktionen beschreiben
1 eFunktion (7 min) 𝕃
Zeichne den Graphen der e-Funktion \(f(x)=e^x\) im Intervall \([-1;3]\). Zeichne in einem Koordinatensystem genau darunter den Graphen der Ableitungsfunktion \(f'(x)\) durch Auftragen der Steigungen an mindestens 5 Stellen. Beschreibe dein Ergebnis und bestimme den Term der Ableitungsfunktion.
| AFB I - K1 K4 K6 | Quelle Holger Engels, Kim Fujan |
2 expFunktion (7 min) 𝕃
Zeichne den Graphen der e-Funktion \(f(x)=2^x\) im Intervall \([-1;3]\). Zeichne in einem Koordinatensystem genau darunter den Graphen der Ableitungsfunktion \(f'(x)\) durch Auftragen der Steigungen an mindestens 5 Stellen. Beschreibe dein Ergebnis.
| AFB I - K1 K4 K6 | Quelle Holger Engels |
3 Trigonometrische Funktionen (8 min) 𝕋 𝕃
Zeichne den Graphen der Sinus-Funktion \(f(x)=sin(x)\) im Intervall \([-2 \pi;2 \pi]\). Zeichne in einem Koordinatensystem genau darunter den Graphen der Ableitungsfunktion \(f'(x)\), indem du die Steigungen an geschickt gewählten Stellen aufträgst. Beschreibe dein Ergebnis und bestimme den Term der Ableitungsfunktion.
Beschreibe ein analoges Vorgehen für \(f_2(x)=cos(x)\) und gib auch den Term für \(f'_2(x)\) an.
| AFB I - K1 K4 K6 | Quelle Holger Engels, Kim Fujan |
4 lnFunktion (7 min) 𝕃
Zeichne den Graphen der ln-Funktion \(f(x)=\ln{x}\) im Intervall \([0;5]\). Zeichne in einem Koordinatensystem genau darunter den Graphen der Ableitungsfunktion \(f'(x)\) durch Auftragen der Steigungen an den Stellen 1, 2, 3, 4. Für deine Beobachtung ist es hilfreich, wenn du die Tangentensteigungen an diesen Stellen exakt kennst. Sie sind:
| x | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| f'(x) | 1 | \(\frac{1}{2}\) | \(\frac{1}{3}\) | \(\frac{1}{4}\) |
Beschreibe dein Ergebnis und bestimme den Term der Ableitungsfunktion.
| AFB I - K1 K4 K6 | Quelle Holger Engels |
5 Verschiebung durch Ableiten (k.A.)
Die in \(\mathbb{R}\) definierte Funktion \(f\) hat die erste Ableitungsfunktion \(f^\prime\) mit \(f^\prime\left(x\right)=2\cdot e^{2x}\) und es gilt \(f\left(0\right)=1\).
Leitet man die erste Ableitungsfunktion \(f^\prime\) ab, so erhält man die zweite Ableitungsfunktion \(f^{\prime\prime}\) von \(f\). Entsprechend entsteht die hundertste Ableitung \(f^{\left(100\right)}\) von \(f\). Der Graph der hundersten Ableitungsfunktion \(f^{\left(100\right)}\) lässt sich aus dem Graphen von \(f\) durch eine Verschiebung in x-Richtung erzeugen.
Ermittle, um wie viele Einheiten der Graph von \(f\) dazu in x-Richtung zu verschieben ist.
| AFB III - K1 K2 K4 K5 | Quelle IQB e.V. | #iqb |
6 Ableitung berechnen und grafisch ermitteln (k.A.) 𝕋 𝕃
Gegeben sind die in \(\mathbb{R}\) definierten Funktionen \(g\) mit \(g\left(x\right)=2\cdot e^x-2\) und \(h\) mit \(h\left(x\right)=e^x+1\). Die Abbildung zeigt ihre Graphen.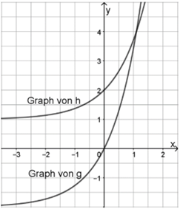
- Die erste Ableitungsfunktion von \(g\) wird mit \(g^\prime\) bezeichnet. Berechne \(g^\prime\left(0\right)\) und veranschauliche in der Abbildung, wie man diesen Wert grafisch ermitteln kann.
- Beurteile folgende Aussage:
Es gibt eine Verschiebung in y-Richtung, durch die der Graph von \(h\) aus dem Graphen von \(g\) erzeugt werden kann.
| AFB II - K1 K2 K4 K5 K6 | Quelle IQB e.V. | #iqb |
