Zum Inhalt springen

Lösung Ableitung berechnen und grafisch ermitteln

Zuletzt geändert von akukin am 2024/10/20 18:31

Teilaufgabe 1

Erwartungshorizont \(g^\prime(x)=2\cdot e^x;\ \ g^\prime(0)=2\)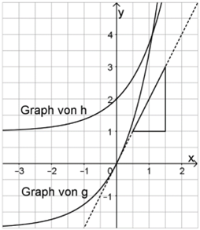 Steigungsdreieck.png
Erläuterung der Lösung

Die Ableitung der Funktionen \(g\) mit \(g(x)=2\cdot e^x-2\) an der Stelle \(x=0\) ist gesucht.

Wir bestimmen zuerst \(g^\prime(x)\):
\(g^\prime(x)=2\cdot e^x\)

Die natürliche Exponentialfunktion ist ihre eigene Ableitung. Der Faktor \(2\) bleibt erhalten (Faktorregel). Der Summand \(-2\) wird beim Ableiten zu \(0\).

Nun können wir \(g^\prime(0)\) ermitteln:
\(g^\prime(0)=2\cdot e^0=2\)
(„Hoch null“ ergibt immer 1.) Steigungsdreieck.png

Die Ableitung an der Stelle \(x=0\) ist die Steigung der Tangente, die den Graphen an dieser Stelle berührt. Also zeichnen wir die Tangente ein (gestrichelte Linie).

Die gesuchte Steigung dieser Tangente wird mit einem passenden Steigungsdreieck veranschaulicht. An diesem ist zu erkennen, dass man tatsächlich 2 Schritte nach oben geht, wenn man 1 Schritt nach rechts gegangen ist. Also ist die Steigung \(g^\prime(0)=2\).

Teilaufgabe 2

Erwartungshorizont Die Aussage ist falsch, da die Steigungen der Graphen von \(g\) und \(h\) an der Stelle \(0\) nicht übereinstimmen.
Erläuterung der Lösung Würde man den Graphen von \(g\) um zwei Längeneinheiten nach oben verschieben, so hätte er tatsächlich denselben y-Achsenabschnitt wie der Graph von \(h\). Jedoch ist die Steigung von \(g\) am y-Achsenabschnitt wesentlich größer als die Steigung von \(h\). Also können die beiden Graphen nur durch vertikales Verschieben nicht zur Deckung gebracht werden. (Man müsste den Graphen von \(g\) noch zusätzlich in y-Richtung stauchen, das heißt den Funktionsterm mit einem Faktor zwischen 0 und 1 multiplizieren.)