Lösung Grafisch Integralwert bestimmen
Zuletzt geändert von akukin am 2024/10/20 16:08
Teilaufgabe 1
Erwartungshorizont
Anzahl der Kästchen: etwa \(8\)\(8\cdot0,25=2\), d. h. der Wert des Integrals ist etwa \(2\).
Erläuterung der Lösung
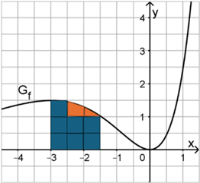\(\int\limits_{-3}^{-1,5}{f\left(x\right)\mathrm{d} x}\)
Anzahl der Kästchen zwischen \(x=-3\) und \(x=-1,5\) zwischen dem Graphen und der x-Achse:
Ungefähr \(7\) ganze Kästchen und \(2\) Teilkästchen, die zusammen etwa ein ganzes ergeben, also insgesamt ca. \(8\) Kästchen.
Jedes Kästchen hat einen Flächeninhalt von \({0,5}^2=0,25\). Folglich hat das gesuchte Integral in etwa den Wert \(8\cdot0,25=2\).Teilaufgabe 2
Erwartungshorizont
Der Graph von \(u\) kann aus \(G_f\) durch Spiegelung an der x-Achse und anschließender Verschiebung um \(2\) in positive y-Richtung erzeugt werden.Hochpunkt: \(\left(0\middle|2\right)\)
Erläuterung der Lösung
Hier geht es um die Transformationen von Funktionen und deren Graphen. Die dazugehörigen Formeln findest du in der Merkhilfe.
Ersetzt man den gesamten Funktionsterm \(f\left(x\right)\) durch \(-f\left(x\right)\), was gleichbedeutend damit ist, dass das Vorzeichen des Funktionswerts umgekehrt wird, dann wird der Graph an der x-Achse gespiegelt (alles, was vorher über der x-Achse war, also positiv, ist jetzt unter der x-Achse, also negativ, und umgekehrt).
Addiert man anschließend zu jedem Funktionswert die Zahl \(2\), so wird jeder Funktionswert um \(2\) größer. Der Graph muss also insgesamt um \(2\) nach oben verschoben werden.
Durch die Spiegelung an der x-Achse wird der ursprüngliche Tiefpunkt \(\left(0\middle|0\right)\) zum Hochpunkt. Durch die Verschiebung um \(2\) nach oben, befindet sich der Hochpunkt am Ende bei \(\left(0\middle|2\right)\).