Lösung Geradenschar
Zuletzt geändert von akukin am 2024/10/01 14:53
Teilaufgabe 1
Erwartungshorizont
Alle Geraden der Schar haben denselben Vektor als Richtungsvektor.Erläuterung der Lösung
Da der Richtungsvektor unabhängig von \(k\) den Wert \(\left(\begin{array}{c} 4 \\ 8 \\ 1 \end{array}\right)\) hat, ist die Richtung von \(g\) bereits bekannt.Teilaufgabe 2
Erwartungshorizont
Da \(\left(\begin{array}{c} 11 \\ 4 \\ 5 \end{array}\right)=s\cdot\left(\begin{array}{c} 4 \\ 8 \\ 1 \end{array}\right)\) für \(s\in\mathbb{R}\) nicht lösbar ist, sind \(O\) und \(P\) keine Eckpunkte, die auf derselben Gerade der Schar liegen.Da \(\left(\begin{array}{c} 11 \\ 4 \\ 5 \end{array}\right) \circ \left(\begin{array}{c} 4 \\ 8 \\ 1 \end{array}\right)=44+32+5\neq0\), sind \(O\) und \(P\) keine benachbarten Eckpunkte, die auf verschiedenen Geraden der Schar liegen.
Erläuterung der Lösung
Der Verbindungsvektor der beiden Punkte ist \(\overrightarrow{OP}=\left(\begin{array}{c} 11 \\ 4 \\ 5 \end{array}\right)\). Dieser ist kein Vielfaches des Richtungsvektors der Geraden, denn die Gleichung \(\left(\begin{array}{c} 11 \\ 4 \\ 5 \end{array}\right)=s\cdot \left(\begin{array}{c} 4 \\ 8 \\ 1 \end{array}\right)\) hat keine Lösung für \(s\in\mathbb{R}\).\(\overrightarrow{OP}\) steht auch nicht senkrecht auf den Geraden, denn das Skalarprodukt aus \(\overrightarrow{OP}\) und dem Richtungsvektor ist
\(\left(\begin{array}{c} 11 \\ 4 \\ 5 \end{array}\right) \circ \left(\begin{array}{c} 4 \\ 8 \\ 1 \end{array}\right)=11\cdot 4+4\cdot 8 + 5\cdot 1 =81 \neq 0\)
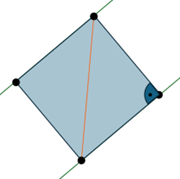Da \(\overrightarrow{OP}\) weder ein Vielfaches des Richtungsvektors der Geraden ist, noch senkrecht auf dem Richtungsvektor steht, müssen die beiden Punkte auf der Diagonalen des Quadrats liegen, sind also nicht benachbart.
(Zwei Seiten des Quadrats liegen ja auf den parallelen Geraden und die anderen zwei Seiten stehen senkrecht auf den Geraden.)