Lösung Dreiecksfläche
Zuletzt geändert von akukin am 2025/08/15 14:20
Das kleinste achsenparallele Rechteck besitzt die Eckpunkte \(A(-1|1), D(5|1), E(5,4) \) und \(F(-1|4) \). Für den Flächeninhalt ergibt sich durch Multiplizieren der Länge und Breite des Rechteckes:
\(F_{Rechteck}=l\cdot b=6\cdot 3=18 \ \text{FE}\).
Um den Flächeninhaltes des Dreieckes \(\Delta ABC\) zu berechnen, ziehen wir vom Flächeninhalt des Rechteckes die Flächeninhalte der drei farbigen Dreiecke ab:
\[\begin{align*} F_{\Delta ABC} &=F_{Rechteck}-F_{grünes Dreieck}-F_{blaues Dreieck}-F_{rotes Dreieck} \\ F_{\Delta ABC} &=18-\frac{1}{2}\cdot \overline{AD}\cdot\overline{BD}-\frac{1}{2}\cdot \overline{BE}\cdot\overline{EC}-\frac{1}{2}\cdot \overline{CF}\cdot\overline{FA}\\ F_{\Delta ABC} &=18-\frac{1}{2}\cdot 6\cdot 1 -\frac{1}{2}\cdot 2 \cdot 3- \frac{1}{2}\cdot 3\cdot 3\\ F_{\Delta ABC} &=18-3-3-4,5=7,5 \ \text{FE}\\ \end{align*}\]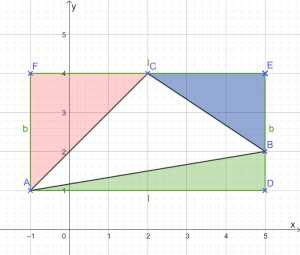
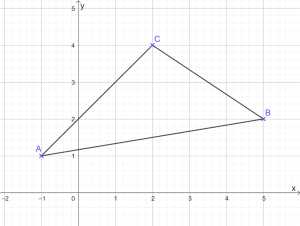
- Um die Dreiecksfläche mit \(F=\frac{1}{2}g\cdot h_g\) zu berechnen, müsste man, um die Länge der Grundseite (\(g\)) zu bestimmen, die Länge der Strecke \(\overline{AB}\) abmessen.
Für die Höhe \(h_g\) müsste man vom Punkt \(C\) ausgehend ein Lot auf die Grundseite \(\overline{AB}\) fällen. Dies könnte man entweder mit dem Geodreieck machen, indem man zwischen Lot und Grundseite einen 90° Winkel abmisst oder aber auch mit einem Zirkel und Lineal konstruieren.
