Lösung Analysis 1
Teilaufgabe a)
Erwartungshorizont
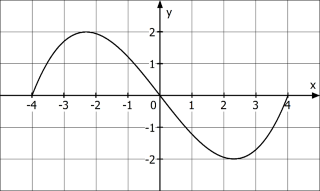
Erläuterung der Lösung

Eine Nullstelle ist durch den Punkt \(N(4|0)\) gegeben. Da der Graph punktsymmetrisch sein soll, muss es bei \(x=-4\) ebenfalls eine Nullstelle geben. Zudem ist durch die Punktsymmetrie festgelegt, dass der Graph durch den Ursprung geht.
Da der Wertebereich \(W_f=[-2;2]\) ist, muss der Hochpunkt bei \(y=2\) liegen und der Tiefpunkt bei \(y=-2\). Die x-Koordinaten sind jedoch nicht bekannt, können also näherungsweise (jedoch symmetrisch) skizziert werden.
Durch die zusätzliche Information \(f^\prime (0)<0\) ist festgelegt, dass der Graph mit negativer Steigung durch den Ursprung verläuft. Folglich müssen der Hochpunkt links und der Tiefpunkt rechts liegen.Teilaufgabe b)
Erwartungshorizont
Möglicher Ansatz: \(g(x)=\sin(bx)\)Periode: \(p=8 \implies b=\frac{2\pi}{8}=\frac{\pi}{4}\)
Damit: \(g(x)=\sin(\frac{\pi}{4}x)\)
Erläuterung der Lösung
Die allgemeine Sinusfunktion hat den Term \(g(x)=a \sin(b(x-c))+d \)Da die Amplitude nicht festgelegt ist, kann \(a=1\) gewählt werden. Eine Verschiebung ist auch nicht notwendig, also \(c=0\) und \(d=0 \).
Ein möglicher Ansatz lautet folglich: \(g(x)=\sin(bx) \)Der Parameter \(b \) ist mit der Periode \(p\) der Sinuswelle verknüpft: \(b=\frac{2\pi}{p}\) Eine Wellenlänge geht von \(x_1=-4\) bis \(x_2=4 \). Die Periode ist also \(p=8\). Eingesetzt ergibt sich \(b=\frac{2\pi}{8}=\frac{\pi}{4}\)
Damit lautet die Funktionsgleichung: \(g(x)=\sin \left(\frac{\pi}{4}x\right)\)