Lösung Stochastik 6 (Problemlöseaufgabe)
Zuletzt geändert von akukin am 2024/12/23 14:45
Analyse:
Indikatoren
- Problem verbalisieren
- Ordnen der Informationen z. B. mithilfe von Skizzen, Modellen, Tabellen
Erwartungshorizont
Problem in eigene Worte fassen oder anhand Skizze darstellen:- Wie sieht ein regelmäßiges Fünfeck aus, in welchem drei von fünf Eckpunkten zu einem Dreieck verbunden sind, dessen Seiten Diagonalen des Fünfecks entsprechen?
- Beispiele:
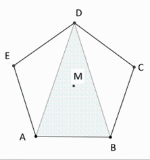
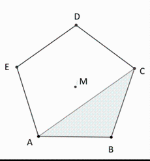
Durchführung:
Indikatoren
- „Einlassen“ auf das Problem
- Untersuchung von Beispielen/Spezialfällen
- Vermutungen äußern
- Lösungsstrategie entwickeln und umsetzen
- (allgemeine) Strukturen finden
- Vermutungen testen/überprüfen
- evtl. Vermutungen ergänzen/anpassen
- evtl. Lösungsstrategien korrigieren
Erwartungshorizont
Wie viele Möglichkeiten gibt es, drei Eckpunkte des Fünfecks als Eckpunkte eines Dreiecks auszuwählen?
z. B.: Untersuchung von Spezialfällen (Strategie 1)
Mit drei nebeneinander liegenden Punkten findet man die Dreiecke ABC, BCD, CDE, ADE und ABE, bei denen M nicht innerhalb des Dreiecks liegt. Dies sind 5 Fälle.
Mit zwei Punkten nebeneinander und einem gegenüber findet man die Dreiecke ABD, BCE, ACD, BDE und ACE, bei denen M innerhalb des Dreiecks liegt. Dies sind ebenfalls 5 Fälle.
ODER z. B.: Systematisches Probieren (Strategie 2)| Eckpunkte des Dreiecks | Mittelpunkt innerhalb? |
|---|---|
| ABC | nein |
| ABD | ja |
| ABE | nein |
| ACD | ja |
| ACE | ja |
| ADE | nein |
| BCD | nein |
| BCE | ja |
| BDE | ja |
| CDE | nein |
Rückblick:
Indikatoren
- Lösung angeben und auf Plausibilität überprüfen/reflektieren
- bei Abbruch: mögliche Gründe reflektieren
- alternative Lösungswege suchen/formulieren
Erwartungshorizont
Folgerung: Die gesuchte Wahrscheinlichkeit beträgt 0,5 bzw. 50 %.
Die Strategien führen jeweils direkt zur gesuchten Wahrscheinlichkeit