2024 eAN - Teil B - Analysis - Aufgabensatz II

Aufgabe 1  Aufgabe 1 𝕋  𝕃

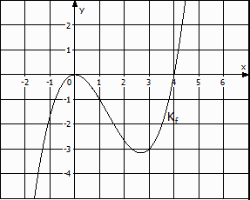
Für eine reelle Zahl \(a\) ist die in \(\mathbb{R}\) definierte Funktion \(f\) gegeben durch \(f(x)=a\cdot x^2\cdot(x-4)\)
Der Graph von \(f\) ist \(K_f\).

1. Ermittle den Wert von \(a\). [2 BE]
2. Berechne die Koordinaten des Tiefpunktes von \(K_f\). [4 BE]
3. Berechne die Größe des Winkels, unter dem die Wendetangente \(w\) an \(K_f\) die x-Achse schneidet. [5 BE]
4. Der Graph der in \(\mathbb{R}\) definierten Funktion \(s\) geht aus \(K_f\) durch Verschiebung um  \(\frac{\mathrm{4}}{\mathrm{3}}\)  in negative x-Richtung sowie eine Verschiebung in y-Richtung hervor. Es gilt \(s\left(x\right)=\frac{1}{3}x^3-\frac{16}{9}x\).
   Zeige unter Verwendung der Funktionsgleichung von \(s^{\prime\prime}\), dass \(K_f\) an der Stelle 1 rechtsgekrümmt ist. [3 BE]
5. Der Ursprung, der Punkt \(P\left(u\middle|0\right)\) und der Punkt \(Q\left(u\middle| f(u)\right)\) bilden für \(0,5\le u\le3,5\) im 4. Quadranten ein Dreieck mit dem Flächeninhalt \(A(u)\).
   Erläutere die Bedeutung der Stelle \(u_1\), die mit folgender Rechnung ermittelt wird:
   \(A^\prime(u_1)=0\ \ \ \Leftrightarrow\ \ \ u_1=3\)
   Dabei gilt: \(A^{\prime\prime}(3)<0\)  und  \(A(0,5)<A(3)\) und \(A(3,5)<A(3)\) [3 BE]
6. Eine quadratische Funktion \(p\) hat dieselben Nullstellen wie \(f\). Die Graphen von \(p\) und \(f\) schließen im 4. Quadranten zwei gleich große Flächenstücke ein. [4 BE]
   Ermittle eine Gleichung von \(p\).
7. Begründe, dass die in \(\mathbb{R}\) definierte Funktion \(h\) mit \(h(x)=e^{f(x)}\) die gleichen Extremstellen wie die Funktion \(f\) hat.[2 BE]