Zum Inhalt springen

Lösung Aufgabe 2

Zuletzt geändert von akukin am 2025/01/14 15:53
Erwartungshorizont (offiziell)

(1) Die Aussage ist wahr. Am Graph K_g ist ersichtlich, dass dieser 5 Stellen mit waagrechter Tangente aufweist.

(2) Die Aussage ist wahr. Zwischen x=0 und x=3 schließt K_g mit der x-Achse eine größere Fläche ein als zwischen x=3 und x=4. Somit ist die Flächenbilanz positiv.

(3) Die Aussage ist falsch. Es gilt J^\prime(x)=g(x). g weist beispielsweise für x=3,5 einen negativen Funktionswert auf. Somit ist J an dieser Stelle nicht monoton wachsend.
Erläuterung der Lösung Aufgabenstellung
Die Abbildung zeigt den Graphen K_g einer Funktion g im Definitionsbereich -4\le x\le4. Entscheide, ob die folgenden Aussagen wahr oder falsch sind. Begründe jeweils deine Entscheidung.
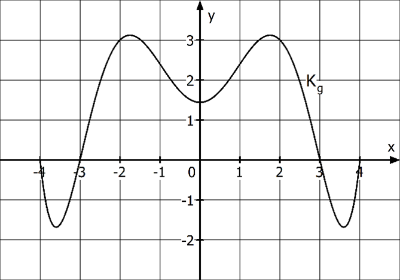
GraphAufgabe2.png
(1) Die zugehörige Ableitungsfunktion g^\prime hat genau 5 Nullstellen.
(2) Es gilt: \int_{0}^{4}{g(x)\mathrm{d} x>0}

(3) Die Integralfunktion J mit J(x)=\int_{0}^{x}{g(t)\mathrm{d} t} ist für 0\le x\le4 monoton wachsend.

Lösung
(1) Die Aussage ist wahr. Am Graph K_g ist ersichtlich, dass dieser 5 Stellen mit waagrechter Tangente aufweist. Und da die Steigung der Tangente die erste Ableitung ist, hat g^\prime genau 5 Nullstellen.
(2) Die Aussage ist wahr. Zwischen x=0 und x=3 schließt K_g mit der x-Achse eine größere Fläche ein als zwischen x=3 und x=4. Die erste Fläche liegt über der x-Achse, also ist das Integral positiv. Die zweite Fläche liegt unter der x-Achse, also ist das Integral negativ. Somit ist die Flächenbilanz positiv.
(3) Die Aussage ist falsch. Ab x=3 wird das Integral kleiner, da die Fläche unterhalb der x-Achse liegt und somit negativ zum Integral beiträgt. Zwar steigt die Integralfunktion bis x=3, aber ab x=3 fällt sie.