Zum Inhalt springen

Lösung Lineare Algebra

Zuletzt geändert von akukin am 2025/01/27 22:41

Teilaufgabe a)

Erwartungshorizont (offiziell) B3.1Lösunga).png
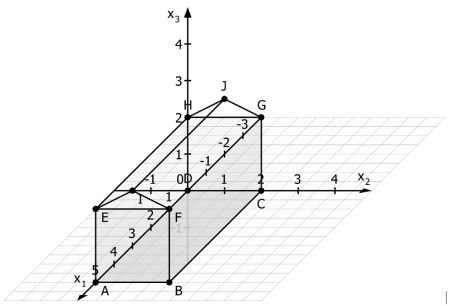
Erläuterung der Lösung Aufgabenstellung

Zeichne das Gewächshaus in ein dreidimensionales Koordinatensystem, wenn die Eckpunkte A(5|0|0),B(5|2|0),C(0|2|0),F(5|2|2),G(0|2|2),I(5|1|2,5) und J(0|1|2,5) bekannt sind.

Lösung

Nachdem die gegebenen Punkte eingezeichnet sind, können die fehlenden Punkt D,E und H durch Symmetrieüberlegungen oder mit Hilfe von Parallelverschiebungen ermittelt werden.

Beachte, dass die x_1-Achse in einem 45°- bzw. 135°-Winkel gezeichnet wird und dass in diese Richtung die Diagonale eines kleinen Kästchens die Länge 1 hat.B3.1Lösunga).png

Teilaufgabe b)

Erwartungshorizont (offiziell) D(0|0|0),E(5|0|2),H(0|0|2)
A_{BCGF}=5\cdot 2=10
A_{ABFE}=2\cdot 2=4
A_{EFI}=\frac{1}{2}\cdot 0,5\cdot 2=0,5
A_{FGJI}=5\cdot \sqrt{1^2+0,5^2}\approx 5,59
A =2\cdot (A_{BCGF}+A_{ABFE}+A_{EFI}+A_{FGJI} )=2\cdot (10+4+0,5+5,59)=40,18
40,18\cdot 10=401,8
Das benötigte Glas wiegt 401,8\text{kg}.
Erläuterung der Lösung Aufgabenstellung

Berechne das Gewicht des für das Gewächshaus benötigten Glases, wenn ein Quadratmeter Glas 10kg wiegt.

Lösung
Die fehlenden Punkte lauten D(0|0|0),E(5|0|2),H(0|0|2).
Jede Form der Glasfläche kommt zweimal vor. Der Flächeninhalt der gesamten Glasfläche A setzt sich zusammen aus:

A =2\cdot (A_{BCGF}+A_{ABFE}+A_{EFI}+A_{FGJI})

Die einzelnen Anteile sind entweder Rechtecke oder Dreiecke. Ihr jeweiliger Flächeninhalt kann mit den bekannten Formeln (siehe Merkhilfe) berechnet werden:
A_{BCGF}=5\cdot 2=10
A_{ABFE}=2\cdot 2=4
A_{EFI}=\frac{1}{2}\cdot 0,5\cdot 2=0,5
Die Länge der Seite FI kann mit Hilfe des Satzes des Pythagoras berechnet werden:

A_{FGJI}=5\cdot \sqrt{1^2+0,5^2}\approx 5,59

Als gesamter Flächeninhalt ergibt sich:
A =2\cdot (A_{BCGF}+A_{ABFE}+A_{EFI}+A_{FGJI} )=2\cdot(10+4+0,5+5,59)=40,18
Das ist der Flächeninhalt in Quadratmetern. Da jeder Quadratmeter 10 kg wiegt, ergibt sich für die gesamte benötigte Masse:
40,18\cdot 10=401,8
Das benötigte Glas wiegt also 401,8\text{kg}.

Teilaufgabe c)

Erwartungshorizont (offiziell) \overrightarrow{JG}=\left(\begin{matrix}0\\1\\-0,5 \end{matrix}\right)
cos(\alpha)=\frac{\left(\begin{matrix}0\\1\\-0,5 \end{matrix}\right)\cdot \left(\begin{matrix}0\\1\\0 \end{matrix}\right)}{\sqrt{1^2+(-0,5)^2}\cdot \sqrt{1^2}}=\frac{1}{\sqrt{1,25}} \approx 0,8944 \quad \ \ \alpha \approx 26,57^\circ
Erläuterung der Lösung Aufgabenstellung

Berechne den Neigungswinkel für eine der schrägen Dachkanten.

Lösung
Der Neigungswinkel ist der Winkel zwischen dem Vektor \overrightarrow{JG} und dem Erdboden, also der x_1x_2-Ebene.
\overrightarrow{JG}=\left(\begin{matrix}0\\1\\-0,5 \end{matrix}\right)

Es gibt zwei Möglichkeiten, den Winkel zwischen einem Vektor und einer Koordinatenebene zu ermitteln:

Option 1:
Man bildet den in die x_1x_2-Koordinatenebene projizierten Vektor (indem man die x_3-Koordinate des Vektors Null setzt) und berechnet anschließend den Winkel zwischen dem ursprünglichen Vektor \overrightarrow{JG} und dem projizierten Vektor \overrightarrow{JG_p} mit Hilfe des (inversen) Kosinus (siehe Merkhilfe):

cos(\alpha)=\frac{\overrightarrow{JG}\cdot \overrightarrow{JG_p}}{|\overrightarrow{JG}|\cdot |\overrightarrow{JG_p}|}=\frac{\left(\begin{matrix}0\\1\\-0,5 \end{matrix}\right)\cdot \left(\begin{matrix}0\\1\\0 \end{matrix}\right)}{\sqrt{1^2+(-0,5)^2}\cdot \sqrt{1^2}}=\frac{1}{\sqrt{1,25}} \approx 0,8944 \quad \ \Leftrightarrow \ \alpha\approx \cos^{-1}(0,8944) \approx 26,57^\circ

Option 2:
Man berechnet den Winkel zwischen dem Vektor \overrightarrow{JG} und dem Normalenvektor der x_1x_2-Ebene und zieht das Ergebnis anschließend von 90° ab.
Manchmal sieht man auch eine Formel für den Winkel zwischen Vektor (bzw. Gerade) und Ebene, in der der Sinus vorkommt. Der Sinus führt dazu, dass man anschließend nicht mehr von 90° subtrahieren muss.

Teilaufgabe d)

Erwartungshorizont (offiziell) Ebene E, in der das Sonnensegel liegt:
E: \vec{x}=\overrightarrow{OF}+r\cdot \overrightarrow{FG}+ s\cdot \overrightarrow{FS}=\left(\begin{matrix}5\\2\\2 \end{matrix}\right)+ r\cdot \left(\begin{matrix}-5\\0\\0 \end{matrix}\right)+ s\cdot \left(\begin{matrix}-2\\2\\-0,5 \end{matrix}\right) \quad \ \ r,s\in \mathbb{R}
2+2s=3 \ \Leftrightarrow \ s=0,5
x_3=2-0,5\cdot 0,5=1,75<1,8 \ \text{(m)} (d. h. der Baumstumpf muss gekürzt werden)
Erläuterung der Lösung Aufgabenstellung

Untersuche, ob der Stumpf gekürzt werden muss, damit das Segel wie geplant gespannt werden kann.

Lösung
Es ist sinnvoll, zuerst eine Ebenengleichung der Ebene aufzustellen, in der das Sonnensegel liegt.
E: \vec{x}=\overrightarrow{OF}+r\cdot \overrightarrow{FG}+ s\cdot \overrightarrow{FS}=\left(\begin{matrix}5\\2\\2 \end{matrix}\right)+ r\cdot \left(\begin{matrix}-5\\0\\0 \end{matrix}\right)+ s\cdot \left(\begin{matrix}-2\\2\\-0,5 \end{matrix}\right) \quad \ \ r,s\in \mathbb{R}
Da der Baumstumpf im Punkt (3|3|0) steht, muss die x_2-Koordinate desjenigen Punktes, der auf der Ebene liegt und sich vertikal über dem Baumstumpf befindet, den Wert 3 haben.
Eingesetzt in die Ebenengleichung (zweite Zeile, x_2-Komponente) ergibt sich:
2+2s=3 \ \Leftrightarrow \ s=0,5
Mit diesem Wert für den Parameter s lässt sich die x_3-Koordinate des entsprechenden Punktes auf der Ebene berechnen. Setzt man s=0,5 in die Ebenengleichung ein, erhält man:
x_3=2-0,5\cdot 0,5=1,75
Das bedeutet, dass das Sonnensegel am Ort des Baumstumpfes eine Höhe von 1,75m hat, während der Baumstumpf selbst 1,8m hoch ist. Folglich muss der Baumstumpf gekürzt werden.

Teilaufgabe e)

Erwartungshorizont (offiziell) \overrightarrow{FS}= \left(\begin{matrix}-2\\2\\-0,5 \end{matrix}\right); \ \ \ |\overrightarrow{FS}|=\sqrt{4+4+0,25}=\sqrt{8,25}
\overrightarrow{GS}= \left(\begin{matrix}3\\2\\-0,5 \end{matrix}\right); \ \ \ |\overrightarrow{GS}|=\sqrt{9+4+0,25}=\sqrt{13,25}
|\overrightarrow{FG}|=5
Erläuterung der Lösung Aufgabenstellung

Zeige, dass es sich bei dem Segel nicht um ein gleichschenkliges Dreieck handelt.

Lösung
Gleichschenklig bedeutet, dass mindestens zwei von drei Seiten gleichlang sind. Mit Hilfe der Beträge der Verbindungsvektoren der Eckpunkte können die Seitenlängen berechnet und verglichen werden.
\overrightarrow{FS}= \left(\begin{matrix}-2\\2\\-0,5 \end{matrix}\right); \ \ \ |\overrightarrow{FS}|=\sqrt{4+4+0,25}=\sqrt{8,25}
\overrightarrow{GS}= \left(\begin{matrix}3\\2\\-0,5 \end{matrix}\right); \ \ \ |\overrightarrow{GS}|=\sqrt{9+4+0,25}=\sqrt{13,25}
|\overrightarrow{FG}|=5
Da alle drei Seiten unterschiedlich lang sind, ist das Sonnensegel kein gleichschenkliges Dreieck.

Teilaufgabe f)

Erwartungshorizont (offiziell) \overrightarrow{FP_k}=\left(\begin{matrix}-2\\k-2\\-0,5 \end{matrix}\right)
|\overrightarrow{FP_k}|=|\overrightarrow{GF}| \ \Leftrightarrow \ 5=\sqrt{4,25+(k-2)^2 }
0=k^2-4k-16,75
k_1\approx 6,56; \ k_2\approx-2,56
D. h. für k_1 ist FGP_k gleichschenklig.

Die Lösung k_2 ist aufgrund des Sachzusammenhangs irrelevant.

Alternativ: Ansatz |\overrightarrow{GP_k}|=|\overrightarrow{GF}| möglich mit k_1\approx 5,97.
Erläuterung der Lösung Aufgabenstellung

Bestimme einen Wert für k, so dass durch die Verschiebung der Pfostenspitze in den Punkt P_k(3|k|1,5) ein gleichschenkliges Dreieck FGP_k entsteht.

Lösung
Die Länge der Seite FP_k des neuen Dreiecks FGP_k kann mit Hilfe des Betrags des Verbindungsvektors zwischen den Punkten F und P_k ermittelt werden.
\overrightarrow{FP_k}=\left(\begin{matrix}-2\\k-2\\-0,5 \end{matrix}\right)
Den Betrag dieses Verbindungsvektors kann man mit der Länge der Seite GF gleichsetzen und die resultierende Gleichung nach k auflösen.

\begin{align} |\overrightarrow{FP_k}| & = |\overrightarrow{GF}| \\ \Leftrightarrow \quad & \sqrt{4,25+(k-2)^2 } = 5 \\ \Leftrightarrow \quad & 4,25+(k-2)^2 = 25 \\ \Leftrightarrow \quad & k^2-4k-16,75 = 0 \\ \Leftrightarrow \quad & k_1 \approx 6,56; \quad k_2 \approx -2,56 \end{align}

D. h. für k_1 ist FGP_k gleichschenklig.

Die Lösung k_2 ist aufgrund des Sachzusammenhangs irrelevant, denn mit einer negativen x_2-Koordinate läge der Pfosten auf der falschen Seite des Glashauses.

Alternativ: Ansatz |\overrightarrow{GP_k}|=|\overrightarrow{GF}| möglich mit k_1\approx5,97.

Teilaufgabe g)

Erwartungshorizont (offiziell) Mit dem Ansatz kann die x_1-Koordinate des Punktes T(t|4|3), der von den beiden Punkten B und G denselben Abstand hat, bestimmt werden.
Erläuterung der Lösung Aufgabenstellung
Zur Lösung einer Aufgabe im Zusammenhang mit den Punkten B und G ergibt sich folgender Ansatz:
\left|\left(\begin{matrix}5-t\\ 2-4\\0-3 \end{matrix}\right)\right| =\left|\left(\begin{matrix}0-t\\ 2-4\\2-3 \end{matrix}\right)\right|

Interpretiere diesen Ansatz.

Lösung
Man kann beide Seiten der Gleichung als Beträge von Verbindungsvektoren auffassen. Die Spitze der Verbindungsvektoren ist identisch, nämlich T(t|4|3). Die Füsse der Verbindungsvektoren sind Punkte, die in der Aufgabe vorkommen. Mit dem Ansatz kann also die x_1-Koordinate des Punktes T(t|4|3), der von den beiden Punkten B und G denselben Abstand hat, bestimmt werden.