- Das Schaubild der Erlösfunktion ist eine Ursprungsgerade mit der Steigung 10.
Um das Schaubild der Erlösfunktion zu zeichnen, erstellen wir (mit dem Taschenrechner) eine Wertetabelle und zeichnen die Punkte ins Koordinatensystem und verbinden sie anschließend.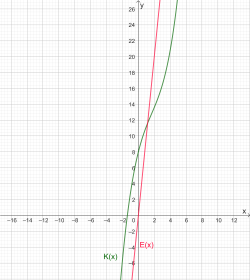
Da sich die Graphen der beiden Funktionen in etwa an den Stellen \(x=1\) und \(x=8\) schneiden, sind Kosten und Erlös an beiden Stellen ungefähr gleich groß.
Alternativ sehen wir auch durch Rechnung, dass die Funktionswerte an beiden Stellen fast gleich groß sind:\[\begin{align} K(1)&=0,2\cdot 1^3-1^2+4\cdot1+8=0,2-1+4+8 \\ &=11,2 \\ &\approx E(1)=10\cdot1=10 \end{align}\]\[\begin{align} K(8)&=0,2\cdot 8^3-8^2+4\cdot8+8=102,4-64+32+8 \\ &=78,4 \\ &\approx E(8)=10\cdot8=80 \end{align}\]Wir erhalten die Gewinnfunktion \(G\), indem wir vom Erlös die Kosten abziehen, das heißt
\[\begin{align} G(x)&=E(x)-K(x) \\ &=10x-(0,2x^3-x^2+4x+8)=10x-0,2x^3+x^2-4x-8 \\ &=-0,2x^3+x^2+6x+8 \end{align}\]Mit einer Wertetabelle können wir feststellen, dass die Funktion \(G(x)\) ihr Maximum bei etwa (5|38) hat (Genauer bei etwa (5,24|38,16)).
Der maximale Gewinn beträgt also 38 GE.
Es gilt \(K_{neu}(1)=10=E(1)\) und \(K_{neu}(8)=80,14\approx 80=E(8)\). Somit sind für 1 ME und 8 ME Kosten und Erlös gleich groß. Die Gewinnzone liegt also unverändert zwischen \(x=1\) und\(x=8\).
Die neue Gewinnfunktion ist
\[\begin{align} G(x)&=E(x)-K(x) \\ &=10x-(1,88x^2-6,9x+15,02)=10x-1,88x^2+6,9x-15,02 \\ &=-1,88x^2+16,9x-15,02 \end{align}\]Wir berechnen die Nullstellen der Funktion \(G(x)\) mit der Mitternachtsformel:
\[\begin{aligned} x_{1,2}&=\frac{-16,9\pm\sqrt{16,9^2-4\cdot(-1,88)\cdot (-15,02)}{2\cdot (-1,88)} \\ &=\frac{-16,9\pm 13,14}{-3,76} \\ x_1&=\frac{-16,9+13,14}{-3,76}=\frac{-3,76}{-3,76}=1 \\ x_2&=\frac{-16,9-13,14}{-3,76}=\frac{-30,04}{-3,76}\approx 7,99 \end{aligned}\]Das Maximum liegt genau zwischen den beiden Nullstellen der Funktion, das heißt an der Stelle \(x=\frac{1+7,99}{2}=4,495\).
\[G(4,495)\approx 22,96\]Der maximale Gewinn beträgt also in etwa 22,96 GE und bleibt somit nicht gleich.
Alternativ kann man den maximalen Gewinn auch wieder mit Hilfe einer Wertetabelle bestimmen.
