Musterklassenarbeit

Aufgabe 1  Musterklassenarbeit Aufgabe 1 𝕃

Der Graph der Funktion \(f\) mit \(f(x)=ax^4\) verläuft durch den Punkt \(P(2|8)\).

1. Bestimme den Wert von \(a\). [2 BE]
2. Gib die Funktionsgleichung an. [1 BE]

Aufgabe 2  Musterklassenarbeit Aufgabe 2 𝕃

Bestimme für die Funktion \(f\) den maximalen Definitionsbereich \(D\) mit zugehörigem Wertebereich \(W\).

1. \(f(x)= x^2+2\)  [2 BE]
2. \(f(x)=-(x-5)^{-2}\)  [3 BE]
3. \(f(x)=x^{-3}\)  [2 BE]

Aufgabe 3  Musterklassenarbeit Aufgabe 3 𝕃

Gegeben ist die Funktion \(f\) mit \(f(x)=-2x^2+16x-31,5\).

1. Berechne das Extremum von \(f\).  [3 BE]
2. Nenne und begründe, ob es sich um ein Maximum oder um ein Minimum handelt.  [2 BE]

Aufgabe 4  Musterklassenarbeit Aufgabe 4 𝕃

Richtig oder falsch? Entscheide und begründe bzw. widerlege durch ein Gegenbeispiel.

1. Jede Potenz von 2 mit ganzzahligem Exponenten ist größer als 2.  [1,5 BE]
2. Jede Potenz einer negativen Zahl ist eine negative Zahl.  [1,5 BE]
3. Jede Potenz einer positiven Zahl mit negativem Exponenten ist negativ.  [1,5 BE]
4. Das Produkt zweier Kubikwurzelterme ist wieder ein Kubikwurzelterm.  [1,5 BE]
5. Die zweite Potenz jeder positiven Zahl ist kleiner als die dritte Potenz der Zahl.  [2 BE]

Aufgabe 5  Musterklassenarbeit Aufgabe 5 𝕃

Bestimme die Lösungen der Gleichung mit Vielfachheiten.

1. \((2x-2)(x+4)=0\) [2 BE]
2. \((x+3)^2=25\) [3 BE]
3. \(3x^2+4=\frac{1}{2}x+4\) [3 BE]
4. \(x^2 (3x^2-10)+3=0\) [6 BE]

Aufgabe 6  Musterklassenarbeit Aufgabe 6 𝕃

Gegeben ist die Funktion \(f\) mit \(f(x)=2x⋅(x^3-5x^2+6x), x\in \mathbb{R}\).

1. Nenne den Grad von \(f\) und die Funktionsgleichung der Vergleichsfunktion \(g\) von \(f\). [2 BE]
2. Gib das Globalverhalten von \(f\) an. [2 BE]
3. Untersuche das Symmetrieverhalten von \(f\). [2 BE]
4. Berechne die Nullstellen von \(f\) mit Vielfachheiten. [4 BE]
5. Skizziere den Graphen von \(f\). [3 BE]

Aufgabe 7  Musterklassenarbeit Aufgabe 7 𝕃

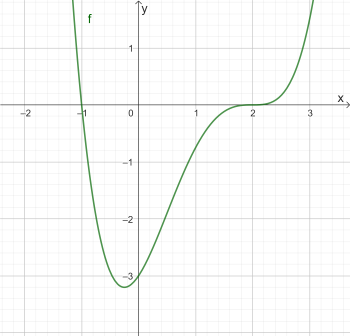
Die Abbildung zeigt den Graphen einer Polynomfunktion \(f\) vierten Grades. Ermittle die Funktionsgleichung von \(f\). [6 BE]

Aufgabe 8  Musterklassenarbeit Aufgabe 8 𝕃

Für eine 18m lange Brücke werden Pfeiler im Abstand von 2m benötigt. Die beiden Pfeiler links und rechts außen haben jeweils eine Länge von 4,5m. Die Brücke wird durch eine quadratische Funktion \(f\) modelliert (\(x, f\) in Metern).

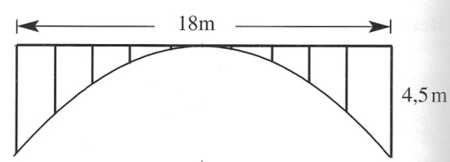
1. Ergänze in der Abbildung ein geeignetes Koordinatensystem. [2 BE]
2. Ermittle die Funktionsgleichung von \(f\). [3 BE]
3. Berechne die gemeinsame Länge der beiden kleinsten Pfeiler. [2 BE]