Zum Inhalt springen

Lösung Graphen beschreiben und skizzieren

Version 8.1 von Frauke Beckstette am 2024/12/18 13:42

f(x)=e^x+2
globales Verhalten:
wenn x \to -\infty dann f(x) \to y=2
wenn x \to \infty dann f(x) \to \infty
Asymptote: y=2
Schnittpunkt mit der y-Achse: S_y(0|3)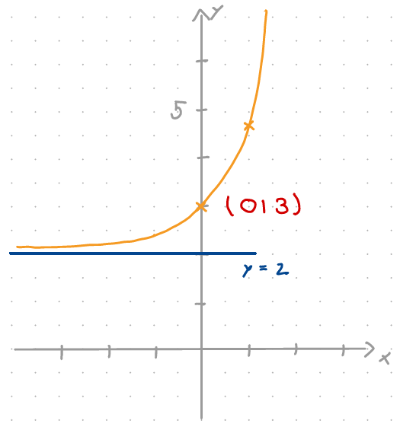
Skizze1.png

g(x)=e^{-x} - 1,5
globales Verhalten:
wenn x \to -\infty dann f(x) \to \infty
wenn x \to \infty dann f(x) \to y=-1,5
Asymptote: y=2
Schnittpunkt mit der y-Achse: S_y(0|-0,5)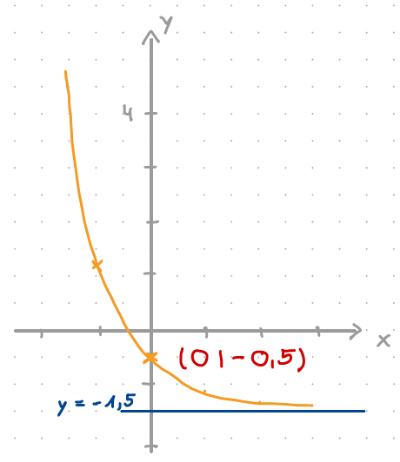
Skizze2.png

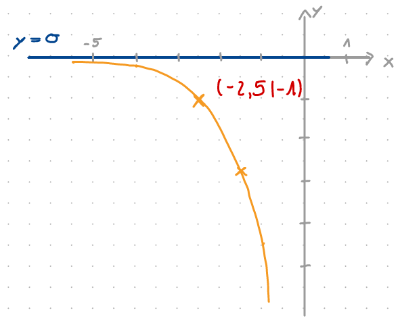
h(x)=-e^{x+2,5}
globales Verhalten:
wenn x \to -\infty dann f(x) \to y=0
wenn x \to \infty dann f(x) \to -\infty
Asymptote: y=2
Schnittpunkt mit der y-Achse: S_y(0|-e^{2,5})
Skizze3.png