BPE 4.6 Wachstums- und Zerfallsprozesse

Aufgabe 1  Wachstum Schokolinsen

Eine 250g Packung Schokolinsen soll nach folgendem Schema an eine Klasse verteilt werden:

1. Ermittle, wie viele Linsen Schüler 3 und Schüler 6 bekommen.
2. In der Packung befinden sich 270 Linsen.
   Bestimme, wie groß die Klasse sein darf, so dass jeder Schüler Linsen bekommt.
3. Eine Klasse hat 30 Schüler. Gib ein zweites Schema an, so dass jeder Schüler gleich viele Linsen erhält.
4. In dem Behälter befinden sich die Schokolinsen für Schüler 10.
   Gib einen Schätzwert für die Anzahl an Linsen für Schüler 10 an.
   Ermittle einen Term, wie man die Zahl der Linsen für Schüler 10 berechnen kann.
5. Bestimme einen Funktionsterm, mit dem du die Anzahl der Linsen für den Schüler an x. - ter Stelle berechnen kannst.

Aufgabe 2  Würfelzerfall 𝕀 

In einem Würfelbecher befinden sich 30 Würfel. Es werden alle Würfel gleichzeitig geworfen. Wenn ein Würfel das Sternsymbol anzeigt, wird er aussortiert. Untenstehend ist das Ergebnis einer Zerfallsreihe zu sehen.

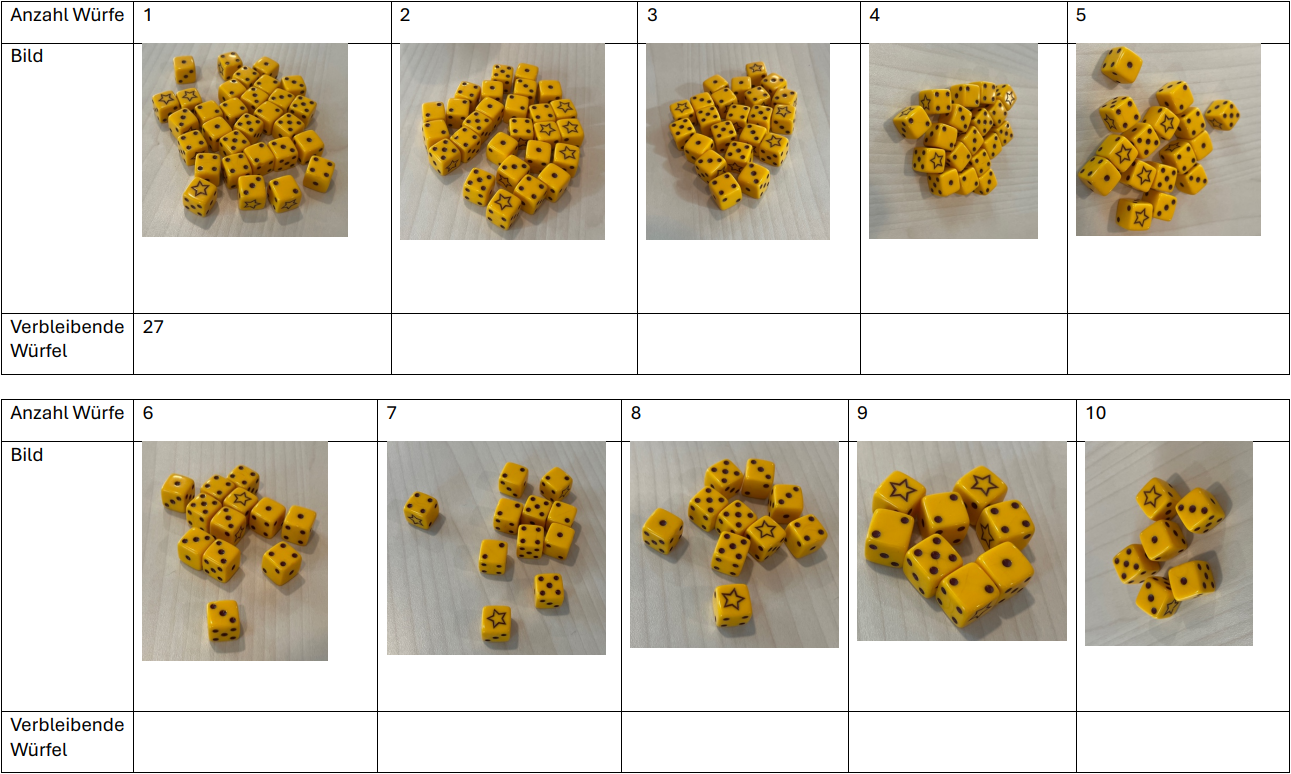
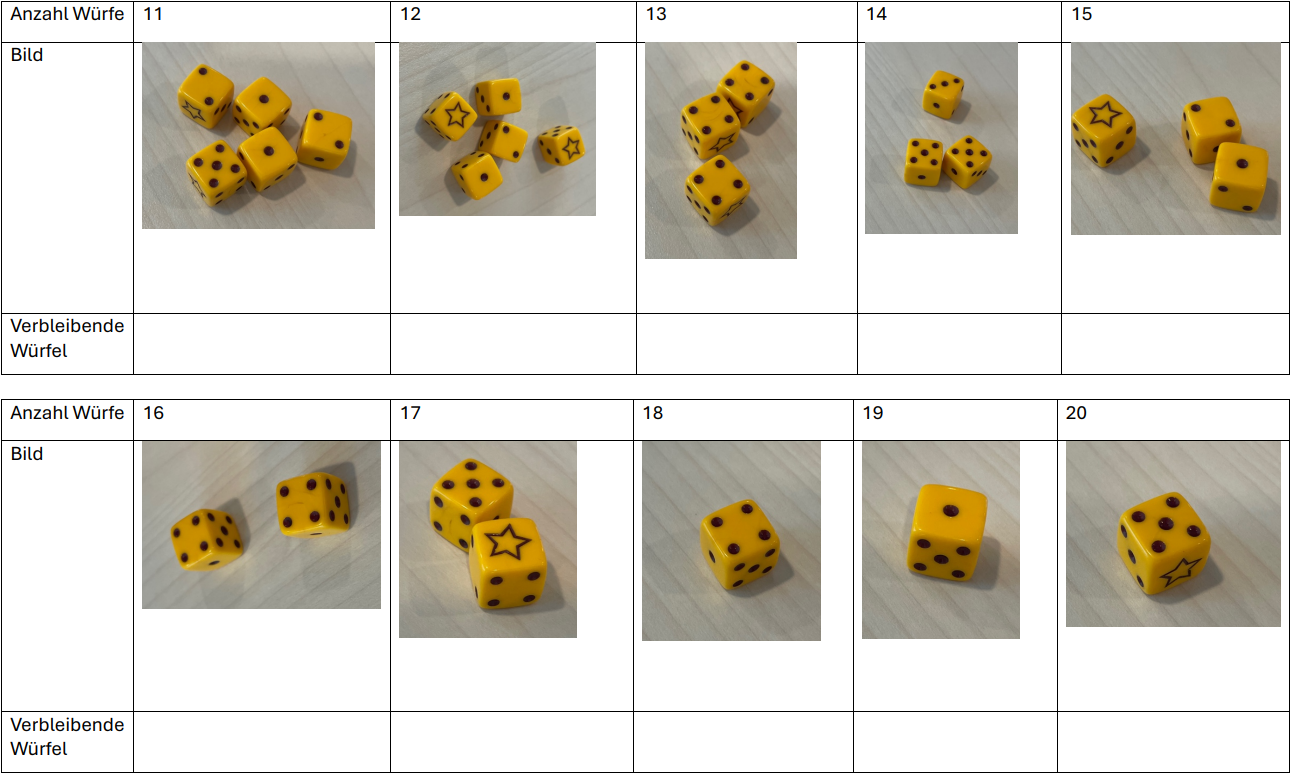
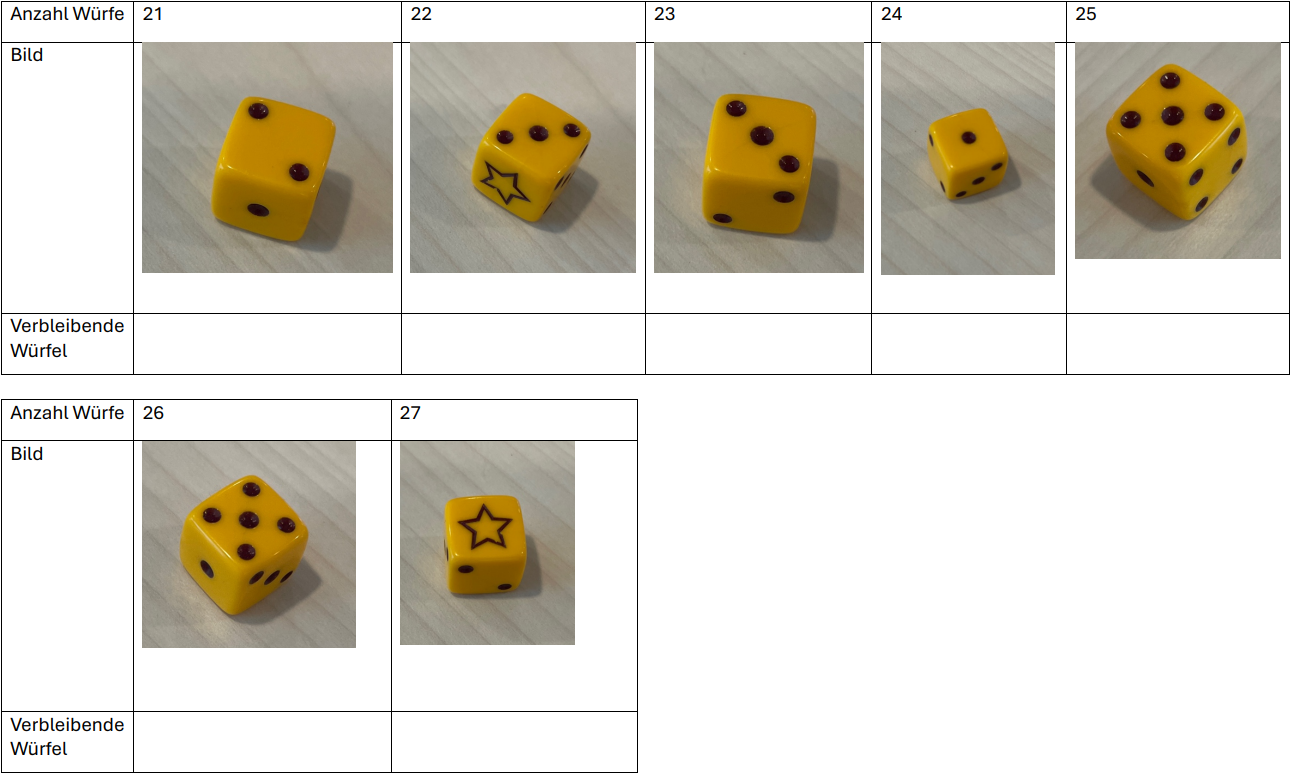
1. Trage die Anzahl der verbleibenden Würfel nach jedem Wurf in die Tabelle ein.
2. Die Wahrscheinleichkeit, dass das Sternsymbol angezeigt wird beträgt .
   Gib eine Funktionsgleichung an, welche die Anzahl der verbleibenden Würfel nach jedem Wurf angibt.
   Beurteile, inwieweit deine Lösung mit den gemessenen Werten übereinstimmt.

Aufgabe 3  Wachstum mit Wertetabelle

Gegeben ist folgende Wertetabelle für einen Wachstumsvorgang,   wird in Stunden angegeben,  gibt den Bestand zum jeweiligen Zeitpunkt  an.

	0	1	2	3	4
			48		768

1. Die Wertetabelle kann ein lineares Wachstum beschreiben.
   Bestimme die fehlenden Werte in der Wertetabelle.
   Ermittle eine passende Funktionsgleichung.
2. Die Wertetabelle kann auch exponentielles Wachstum beschreiben.
   Bestimme eine Funktionsgleichung in der Form
3. Zeige, dass  ebenfalls zur Wertetabelle passt.
4. Gib an, nach welcher Zeit sich der Anfangsbestand verdoppelt.

Aufgabe 4  Abkühlprozesse

Die Temperatur eines Getränks  nach einer Zeit  in Minuten kann mit folgender Formel  ermittelt werden. Dabei bezeichnet  die Umgebungstemperatur,  die Anfangstemperatur und  die Abkühlrate.
 soll 20°C betragen.
Der Abkühlprozess von Tee wird in verschiedenen Gefäßen aus verschiedenen Materialien untersucht. In einer Keramiktasse kann die Temperatur  nach  Minuten durch die Funktionsgleichung  berechnet werden.

1. Welche Anfangstemperatur hat der Tee?
2. Wird der Tee mit der selben Anfangstemperatur in einen Thermobecher bzw. in eine Tasse aus Glas geschüttet, verläuft der Abkühlprozess anders. Erläutere, wie sich die Parameter in der Funktionsgleichung  ändern müssen, wenn das Getränk.
3. Idee: evtl noch Schaubilder zuordnen lassen mit k=0,05 (Thermobecher) und k = 0,15 (Glas)

Aufgabe 5  Linear oder exponentiell 𝕃

Ordne zu!

Aufgabe 6  Anwendung und Darstellungsformen

Gegeben ist die folgende Funktionsgleichung  in Stunden.

1. Beschreibe einen Anwendungskontext, welcher mit der Funktionsgleichung modelliert werden kann.
2. Beurteile, ob die Funktionsgleichung  ebenfalls diesen Prozess beschreibt.
3. Gib an, wie die Funktionsgleichung verändert werden muss, wenn  in Minuten gemessen wird.

Aufgabe 7  CO2-Konzentration (eAN) 𝕃

In einer Messstation wird seit 1958 kontinuierlich die CO₂-Konzentration in der Luft gemessen, die in ppm (parts per million) angegeben wird. Die Tabelle gibt für die Jahre 1960, 1985 und 2010 jeweils den jährlichen Durchschnittswert der Messwerte an.

1. Die jährlichen Durchschnittswerte haben sich im Zeitraum von 1960 bis 1985 in guter Näherung exponentiell entwickelt. Ermittle die zugehörige jährliche Wachstumsrate in Prozent. (zur Kontrolle: etwa 0,35%)
2. Berechne unter der Annahme, dass sich das exponentielle Wachstum nach 1985 in gleicher Weise fortgesetzt hat, den jährlichen Durchschnittswert für das Jahr 2010. Vergleiche diesen Wert mit dem zugehörigen Wert aus der Tabelle und formuliere das Ergebnis deines Vergleichs im Sachzusammenhang.

#iqb

Aufgabe 8  Radioaktiver Zerfall (eAN) 𝕃

Am 26. April 1986 ereignete sich in der Ukraine ein Reaktorunfall, bei dem radioaktives Plutonium-241 freigesetzt wurde. Plutonium-241 zerfällt exponentiell, d. h. in jedem Jahr nimmt die Masse des vorhandenen Plutonium-241 um einen konstanten prozentualen Anteil ab.

Im Folgenden wird der Zerfall einer bestimmten Menge Plutonium-241 betrachtet. Dieser Zerfall wird durch die Funktion  mit  und  beschrieben. Dabei ist  die Zeit in Jahren, die seit dem Reaktorunfall vergangen ist, und  die Masse des verbliebenen Plutonium-241 in Milligramm.

1. Gib die Bedeutung des Faktors 200 im Sachzusammenhang an und berechne den prozentualen Anteil, um den die Masse des Plutonium-241 in jedem Jahr abnimmt.
2. Bestimme das Jahr, in dessen Verlauf erstmals weniger als ein Milligramm des Plutonium-241 vorhanden sein wird.

#iqb