Inhalt
K4 K5 Ich kann Werte der Tangentensteigung graphisch bestimmen
K4 K1 Ich kann aus Werten der Tangentensteigung einen Graphen zeichnen und diesen als Graphen der Ableitungsfunktion deuten
K6 Ich kann Zusammenhänge zwischen den beiden Funktionsgraphen beschreiben
K4 K1 Ich kann erste Hypothesen über einen möglichen algebraischen Zusammenhang zwischen Funktion und Ableitungsfunktion entwickeln
- Punktweise graphisch ableiten
- Qualitativ graphisch ableiten
- Zusammenhänge HP, TP, SP vorwärts und rückwärts
- Funktionsterm der Ableitungsfunktion aus Tangentensteigungen aufstellen
- Beobachtungen bei e^x
Es ist das Schaubild \(K_f\) einer Funktion \(f\) gegeben. Kennzeichne Punkte auf \(K_f\), für die gilt:
- die Steigung der Tangente in diesem Punkt ist 1
- die Steigung der Tangente in diesem Punkt ist -1,5
- die Steigung der Tangente in diesem Punkt ist 0

| AFB II - K2 K4 K5 | Quelle Stephanie Wietzorek und Simone Kanzler |
Skizziere das Schaubild der Steigungsfunktion.

| AFB II - K1 K4 K5 | Quelle Stephanie Wietzorek, Simone Kanzler |
Ein Auto soll auf freier Autobahn auf \(180\frac{km}{h}\) beschleunigen. Die Geschwindigkeit wird annähernd durch \(v(t)=180\cdot(1-e^{-0,1t})\) beschrieben. \(v(t)\) beschreibt hierbei die momentante Geschwindigkeit zum Zeitpunkt \(t\) in Sekunden. Der Verlauf der Geschwindigkeit ist dem Schaubild zu entnehmen.

- Zu welchem Zeitpunkt wird die Höchstgeschwindigkeit von \(180\frac{km}{h}\) erreicht?
- Wann ist die Beschleunigung am höchsten?
- Skizziere ein Schaubild, aus welchem die Beschleunigung zum Zeitpunkt t hervorgeht.
| AFB II - K1 K3 K4 K6 | Quelle Stephanie Wietzorek, Simone Kanzler |
Ordne jedem Funktionsgraph (grün) den Graphen ihrer Steigungsfunktion (blau) zu. Begründe deine Zuordnung.
Das blaue Schaubild zeigt eine Funktion, das rote Schaubild zeigt ihre Steigungsfunktion.
- Bestimme die Gleichungen der beiden Schaubilder.
- Welchen Grad besitzen die beiden Funktionen?
- Stelle eine Hypothese auf, welchen Grad die Steigungsfunktion einer Funktion 4. Grades hat und überlege dir, wie du die Hypothese überprüfen kannst.
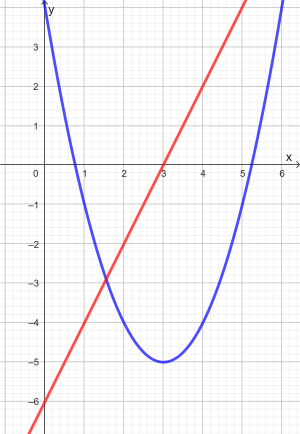
| AFB III - K1 K2 K4 K5 | Quelle Stephanie Wietzorek, Simone Kanzler |
- Skizziere eine mögliche Parabel 2. Grades, welche eine waagrechte Tangente an der Stelle \(x = -2\) hat. Welche Gemeinsamkeiten haben alle Parabeln mit dieser Eigenschaft?
- Skizziere das Schaubild einer möglichen Funktion, welches drei waagrechte Tangenten besitzt. Welchen Grad hat diese Funktion mindestens?
- Eine Funktion f hat nur positive Steigungen. Skizziere das Schaubild einer möglichen Funktion.
- Es ist ein achsensymmetrisches Schaubild einer Funktion 4. Grades gesucht. Folgende Angaben sind bekannt, fülle die Lücken und skizziere das Schaubild der Funktion.
| x | -4 | -1 | 0 | 1 | 4 |
| Funktionswert | -2,5 | | 2 | 0 |
|
| Tangentensteigung | -2 | | 0 | -1 |
|
| AFB III - K2 K4 K5 | Quelle Stephanie Wietzorek, Simone Kanzler |
Prüfe die Aussagen! Welche sind wahr? Eine Polynomfunktion 3. Grades ..
☐ hat immer zwei Extrempunkte!
☐ kann auch mal nur einen Extrempunkt haben!
☐ kann auch mal keinen Extrempunkt haben!
☐ hat immer genau einen Wendepunkt!
☐ hat entweder einen Sattelpunkt oder zwei Extrempunkte!
Gegeben ist das Schaubild einer Funktion. Nimm Stellung zu folgenden Aussagen und begründe deine Antwort.

☐ die Tangentensteigungen sind negativ für \(x \in ]2;5[\)
☐ die Steigung der Tangente an der Stelle \(x = 1\) ist kleiner als \(-2\)
☐ an der Stelle \(x = 2\) liegt eine waagrechte Tangente
☐ die Funktionswerte sind positiv für \(-4 < x < 2\)
☐ die Tangentensteigungen haben einen Vorzeichenwechsel bei \(x=-4\) von ⊝ ⇾ ⊕
| AFB I - K1 K4 K5 K6 | Quelle Stephanie Wietzorek, Simone Kanzler |
Welche Aussagen treffen auf eine Sattelstelle zu?
☐ Eine Sattelstelle hat eine waagrechte Tangente.
☐ An einer Sattelstelle hat die Steigungsfunktion ein Maximum oder ein Minimum.
☐ An einer Sattelstelle gibt es immer auch einen Krümmungswechsel.
☐ Eine Sattelstelle ist auch eine Wendestelle.
☐ Eine Sattelstelle kann auch eine Maximalstelle sein.
| AFB III - k.A. | Quelle KMap |
Kompetenzmatrix und Seitenreflexion
| K1 | K2 | K3 | K4 | K5 | K6 |
|---|
| I | 2 | 0 | 0 | 4 | 3 | 1 |
| II | 3 | 2 | 1 | 4 | 2 | 2 |
| III | 1 | 2 | 0 | 2 | 2 | 0 |
Bearbeitungszeit gesamt: 60 min
| Abdeckung Bildungsplan | | |
|---|
| Abdeckung Kompetenzen | | |
|---|
| Abdeckung Anforderungsbereiche | | |
|---|
| Eignung gemäß Kriterien | | |
|---|
| Umfang gemäß Mengengerüst | | |
|---|