Vorschlag einer Klassenarbeit
Zuletzt geändert von akukin am 2025/08/14 16:05
1 KA1 Punkte: 6 (6 min)
Gegeben sind die Punkte\(A(1|2|3), B(3|-2|1), C(0|4|-1)\).
- Bestimme die Vektoren \(\vec{AB}, \vec{BC}\) und \( \vec{CA} \).
- Untersuche, welche der drei Vektoren \(\vec{AB}, \vec{BC} \) und \(\vec{CA} \) zueinander orthogonal sind.
| AFB I - K3 K5 | Quelle Dirk Tebbe |
2 KA2 Punkte: 6 (6 min)
Gegeben sind die Punkte\(P(3|-1|2), Q(1|2|-1)\) und \(R(0|4|-1)\).
- Berechne den Mittelpunkt der Strecke \(\overline{PQ}\).
- Spiegel den Punkt \(P\) am Koordinatenursprung und gibt den Bildpunkt \(P' \) an.
- Spiegel den Punkt \(Q\) an der \(x_1x_2\)-Ebene und gibt den Bildpunkt \(Q' \) an.
- Spiegel den Punkt \(R\) am Punkt \(Z(2|1|0)\) und gibt den Bildpunkt \(R' \) an.
| AFB I - K3 K5 | Quelle Dirk Tebbe |
3 KA3 Punkte: 7 (9 min)
- Skizziere ein Parallelogramm \(ABCD\).
- Ergänze die Koordinaten der vier vorgegebenen Punkte \(A, B, C\) und \(D\) so, dass das Viereck \(ABCD\) ein Parallelogramm ist
\( A(2|1|a_3), B(5|0|1), C(9|c_2|6)\) und \(D(d_1|1|8)\).
| AFB I - K3 K5 | Quelle Dirk Tebbe |
4 KA4 Punkte: 9 (11 min)
Gegeben ist das Dreieck \(ABC\) mit \( A(5|9|1), B(1|2|5)\) und \( C(9|-2|6)\).
- Zeige, dass das Dreieck gleichschenklig und rechtwinklig ist.
- Berechne den Flächeninhalt der Dreiecksfläche.
- Ergänze das Dreieck \(ABC\) mit einem Punkt \(D\) zu einem Quadrat. Gib den Punkt \(D\) an.
| AFB I - K3 K5 | Quelle Dirk Tebbe |
5 KA5 Punkte: 12 (13 min)
Die Figur zeigt eine Pyramide mit quadratischer Grundfläche und der Höhe 6 cm. Die Grundfläche der Pyramide hat die Seitenlänge 4 cm.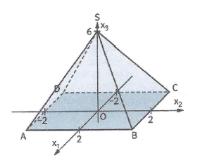
- Gib die Koordinaten der Punkte \(A, B, C\) und \(D\) an.
- Berechne das Volumen der Pyramide.
- Berechne den Flächeninhalt einer Seitenfläche.
- Berechne die Größe des Winkels \(\alpha\), den die Seitenkanten \(SB\) und \(SC\) miteinander einschließen.
| AFB I - K3 K5 | Quelle Dirk Tebbe |
