Mathebrücke Anforderungsbereich II
Klasse 8
BPE 1.1 Rechnen mit Termen
Aufgabe 1 Aufstellen von Termen - Pizza-Party 𝕃
Kim, Sasha und Marvin organisieren zusammen eine große Party. Sie bestellen bei einem Pizzaservice 18 Pizzen. Nach der Party zählen die drei Freunde, dass 11 Pizzaschachteln leer, 5 noch halb voll und 2 Schachteln ganz voll sind. Da alle auch gerne eine kalte Pizza essen, möchten sie die Pizzaschachteln so untereinander aufteilen, dass jeder gleich viel bekommt. Ermittle, wie viele Pizzaschachteln jeder dann bekommt.
| AFB II | Kompetenzen K3 K4 K5 K6 | Bearbeitungszeit 7 min |
| Quelle Team Mathebrücke | Lizenz k.A. | |
Aufgabe 1 Binomische Formeln mal anders 𝕃
Trage jeweils ein, welche Werte für die Symbole eingesetzt werden müssen, so dass die Termumformung richtig ist.
| a) \((x + \square)(x - \square) = x^2 - 25\) | \(\square=\) |
| b) \((2x - \square)^2 = 4x^2 - \Delta + 9\) | \(\square=\) \(\Delta=\) |
| c) \((x - \square)^2 = x^2 - 4xy + \Delta\) | \(\square=\) \(\Delta=\) |
| d) \((2z - \square)^2 =\heartsuit -8z + \Delta\) | \(\square=\) \(\Delta=\) \(\heartsuit=\) |
| e) \((4x - \square)(4x + \square) = \Delta - 49y^2\) | \(\square=\) \(\Delta=\) |
| AFB II | Kompetenzen K5 | Bearbeitungszeit 5 min |
| Quelle Team Mathebrücke | Lizenz k.A. | |
Aufgabe 2 Algebraische Begriffe 2 𝕃
Bestimme einen Rechenausdruck: Multipliziere die Differenz der Zahlen 31 und 12 mit 20, addiere dazu das Produkt der Zahlen 35 und 7 und subtrahiere vom Ergebnis die Differenz der Zahlen 45 und 20.
| AFB II | Kompetenzen K4 K5 | Bearbeitungszeit 4 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
BPE 2.1 Äquivalenzumformungen
Aufgabe 3 Ungleichungen lösen 𝕃
- Peter sammelt für die Klassenkasse Geld ein. Zu Beginn hat er 3 €. Anschließend sammelt er 1,50€ pro Person ein. Berechne, aus wie vielen Personen die Klasse mindestens besteht, wenn er am Ende mehr als 35 € in der Klassenkasse hat?
- Ermittle die Lösung grafisch und rechnerisch \(-2x+3<5\)
| AFB II | Kompetenzen K1 K5 | Bearbeitungszeit 7 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 4 Zuordnen 𝕃
Ein Modegeschäft bietet auf Jeans einen Preisnachlass von 20% an.
Gib zu jedem Berechnungswunsch von Susi die zugehörige Formel an. Erläutere die Unterschiede.
| Text | Berechnung |
|---|---|
| Susi möchte wissen, wie hoch der Preisnachlass für eine Jeans im Wert von 90€ ist | \( G = 72 \cdot \frac{100}{20} \) |
| Susi möchte den reduzierten Preis einer Jeans im Wert von 90€ wissen | \( P = 90 \cdot \frac{20}{100} \) |
| Susi möchte den regulären Preis wissen, wenn der reduzierte Preis 72€ beträgt | \( 90 - 90 \cdot \frac{20}{100}\) |
| AFB II | Kompetenzen K4 K5 K6 | Bearbeitungszeit 6 min |
| Quelle Simone Kanzler, Stephanie Wietzorek | Lizenz CC BY-SA | |
Aufgabe 4 Rabatt-Aktion bei Madio-Markt 𝕃
Der Elektronik-Discounter Madio-Markt startet eine Rabatt-Aktion unter dem Motto „Alles 19 % billiger!“. Tatsächlich wird in der Rabatt-Woche alles zum Netto-Preis, also ohne die 19 % Mehrwertsteuer verkauft.
Klara denkt: „Da stimmt doch was nicht. Ich bin doch nicht doof!“
Begründe, ob Klara recht hat.
| AFB II | Kompetenzen K1 K5 K6 | Bearbeitungszeit k.A. |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 4 Zinssätze 𝕃
Bastian legt 10000 € bei der Bank an.
Nach drei Jahren beträgt sein Guthaben 10841,13 €.
Bastian weiß, dass der Zinssatz für das dritte Jahr 4 % betragen hat.
Die Zinssätze für das erste und zweite Jahr kennt er nicht.
- Berechne, wie viel Guthaben Bastian nach dem zweiten Jahr hatte?
- Ermittle, wie hoch der Zinssatz im ersten und im zweiten Jahr sein muss, wenn in beiden Jahren der Zinssatz gleich war?
- Berechne, wie hoch die Zinssätze im ersten und im zweiten Jahr sein müssen, wenn der Zinssatz im zweiten Jahr doppelt so hoch war wie im ersten Jahr?
| AFB II | Kompetenzen K5 K4 | Bearbeitungszeit k.A. |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 4 arbeitendes Geld 𝕃
Stell dir vor, du bekommst jeden Monat Taschengeld. Normalerweise gibst du es für Snacks, Apps oder neue Skins aus - klar. Aber was wäre, wenn dein Geld für dich arbeitet, während du chillst, zockst oder TikToks schaust.
Charlotte, Kim, Anton und Joel unterhalten sich in der Pause darüber, wie sie ihr Geld für sich arbeiten lassen können. Die Eltern fanden die Idee, das Taschengeld zu sparen, super und haben den Schülern folgende Angebote gemacht:
Charlotte bekommt 25€ Taschengeld im Monat. Ihre Eltern bieten ihr an, am Ende des Jahres 10% Zinsen oben drauf zu geben.
Kim bekommt im Monat 28€ Taschengeld und würde am Ende des Jahres 1% weniger Zinsen bekommen wie Charlotte.
Anton bekommt 30€ Taschengeld. Am Ende des Jahres würde er insgesamt von seinen Eltern 370€ bekommen.
Joel bekommt am Ende des Jahres von seinen Eltern mit 8% Zinsen insgesamt 349,92€, welches sie selbstverständlich auf 350€ aufrunden.
- Erläutere, wie das Geld für die vier Freunde arbeitet.
- Begründe, welches Angebot du am besten fändest?
- Ein Jahr Sparen ist Joel zu lange. Er möchte die neue Switch Lite für 339 € kaufen, die in 4 Monaten rauskommt. Die Eltern bieten ihm eine Verkürzung des Sparzeitraums an, zahlen in diesem Fall die Zinsen aber nur anteilig aus. Begründe, dass er die Switch zu diesem Zeitpunkt noch nicht kaufen kann.
- Berechne, wie viele Tage Joel mindestens sparen muss, damit sein Geld inklusive Zinsen ausreicht, um die Switch zu kaufen?
| AFB II | Kompetenzen K1 K2 K3 K5 K6 | Bearbeitungszeit k.A. |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
BPE 3.1 Funktionaler Zusammenhang
Aufgabe 6 Weg-Zeit-Diagramme interpretieren und beschreiben 𝕃
 Anna besucht ihre Freundin zu Fuß.
Anna besucht ihre Freundin zu Fuß.
- Interpretiere das Diagramm.
- Beschreibe, wie das zugehörige Diagramm aussieht, wenn Anna mit dem Fahrrad zu ihrer Freundin fährt und dort 1 Stunde bleibt. Begründe deine Antwort mit Hilfe der Darstellung eines möglichen Diagramms.
| AFB II | Kompetenzen K1 K4 | Bearbeitungszeit 12 min |
| Quelle Team Mathebrücke | Lizenz k.A. | |
Aufgabe 6 Marathon 𝕃
 Paul läuft einen Marathon. Beurteile, ob die Aussagen wahr oder falsch sind. Begründe deine Entscheidung.
Paul läuft einen Marathon. Beurteile, ob die Aussagen wahr oder falsch sind. Begründe deine Entscheidung.
- Paul läuft am Anfang schneller als am Ende.
- Er läuft 2,5 Stunden.
- Er macht nach 130 Minuten eine Pause.
- Er wird mit der Zeit langsamer.
- Er legt 40 km zurück.
| AFB II | Kompetenzen K1 K4 | Bearbeitungszeit 6 min |
| Quelle Team Mathebrücke | Lizenz k.A. | |
Aufgabe 7 Wertetafeln 2 𝕃
Bestimme die fehlenden Werte der folgenden Wertetafeln, die zu linearen Funktionen gehören:
\(x\) -1 0 1 2 3 4 \(y\) 3 0 -3 \(x\) 2 4 6 8 10 12 \(y\) 0 0,5 \(x\) 1 2 3 4 5 6 \(y\) -3,5 -2
| AFB II | Kompetenzen K5 | Bearbeitungszeit 6 min |
| Quelle Team Mathebrücke | Lizenz k.A. | |
Aufgabe 8 Achsen ergänzen 𝕃
In nebenstehender Abbildung sind zwei Geraden dargestellt.
Eine der beiden Geraden hat die Gleichung \(y=\frac{1}{4}x+2\), die andere hat den y-Achsenabschnitt \(-4\).
- Zeichne ein mögliches zugehörendes Koordinatensystem mit Achsenskalierung ein.
- Bestimme die Gleichung der zweiten Geraden.
| AFB II | Kompetenzen K2 K4 K5 | Bearbeitungszeit 5 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 8 Zeichnen von Geraden 𝕃
Zeichne die Gerade mit der Gleichung \(y=a\cdot(x-2)+3\) für
- \(a=1\)
- \(a=-1\)
- \(a=\frac{1}{2}\)
- \(a=-\frac{3}{4}\)
| AFB II | Kompetenzen K4 K5 | Bearbeitungszeit 7 min |
| Quelle Team Mathebrücke | Lizenz k.A. | |
Aufgabe 9 Lineare Gleichungen lösen 𝕃
Begründe für jede der folgenden Aufgabenstellungen, ob sie zu der Gleichung \(3x+2=0\) führt.
- Berechne den Schnittpunkt der Geraden \(g: \ y=3x+2\) mit der x-Achse.
- Berechne den Schnittpunkt mit der y-Achse der Geraden mit der Gleichung \(y=3x+2\).
- Berechne den Schnittpunkt der Geraden h mit der Gleichung \(y=3x+2\) und der Geraden g mit \(g: \ y=0\).
| AFB II | Kompetenzen K1 | Bearbeitungszeit 5 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 9 Geradengleichungen bestimmen 𝕃
- Bestimme die Gleichungen der beiden Geraden.
- Bestimme die Schnittpunkte der beiden Geraden mit der x-Achse.
| AFB II | Kompetenzen K4 K5 | Bearbeitungszeit 11 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 10 Der PC-Boom 𝕃
Der PC-Boom
Die Zahl weltweit abgesetzter Computer (in Millionen) nimmt rasant zu:
Weltweit abgesetzte Personal Computer:
| 2004 | 2005 | 2006 | 2007 | 2008 | 2009 |
| 190 | 212 | 240 | 273 | 291 | 306 |
- Bestimme einen linearen Funktionsterm, der diese Entwicklung annähernd beschreibt.
- Triff auf Grund deines Ergebnisses aus a) eine Prognose für die Anzahl der weltweit abgesetzten Computer im Jahr 2013.
| AFB II | Kompetenzen K4 K5 K6 | Bearbeitungszeit 8 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 10 Mietwagenpreise
Frau Martin hat sich einen Mietwagen genommen und ist damit 140 Kilometer gefahren. Sie erhält eine Rechnung über 124,00 Euro. Dieser Wert beinhaltet eine Tagespauschale und einen Kilometerpreis. Herr Martin mietet denselben Wagen am nächsten Tag und fährt damit 80 km. Er muss 88,00 Euro bezahlen. Die Tochter der Familie Martin hatte sich den Wagen auch schon einmal für 180,00 Euro gemietet. Sie fuhr 200 km. Sie vergleicht ihre Kosten mit den Rechnungen ihrer Eltern. Beurteile, ob sie zu Recht verärgert ist.
| AFB II | Kompetenzen K3 K4 K5 | Bearbeitungszeit 7 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 11 Wertetabellen prüfen 𝕃
Beurteile, ob folgende Zuordnungen eine lineare Funktion darstellen. Begründe deine Antwort.
Zusatz (aus BPE 3.5): Gib – wenn möglich – die Funktionsgleichung an.
\(x\) 0 1 2 3 4 5 \(f(x)\) 1,5 3 4,5 6 7,5 9 \(x\) -2 -1 0 1 2 3 \(g(x)\) 4,5 2 -0,5 -3 -5,5 -8 \(x\) 0 3 4 10 12 13 \(h(x)\) 2,5 7 8,5 17,5 20,5 22 \(x\) 0 2 4 6 8 10 \(i(x)\) 0 4 16 36 64 100 \(x\) 0 1 4 6 8 11 \(j(x)\) 40 35 20 10 0 -15 \(x\) -2 0 1 3 7 15 \(k(x)\) 1 0 -0,5 -1,5 -3,5 -7,5 \(x\) -4 -1 1 3 6 7 \(l(x)\) 69 3 9 55 199 267
| AFB II | Kompetenzen K4 K5 | Bearbeitungszeit 10 min |
| Quelle Team Mathebrücke | Lizenz k.A. | |
Aufgabe 11 Zuordnungsaufgabe Funktionsterm und Schaubild 𝕃
Ordne den Schaubildern zu:
a) \(y=-\frac{3}{4}x+2\) b) \(y=\frac{1}{3}x\) c) \(y=-\frac{4}{3}x+2\) d) \(y=3x\)
1)  | 2) |
3)  | 4)  |
| AFB II | Kompetenzen K4 K5 | Bearbeitungszeit 7 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 11 Geradengleichungen bestimmen 𝕃
- Bestimme die Gleichungen der beiden Geraden.
- Bestimme die Schnittpunkte der beiden Geraden mit der x-Achse.
- Gib die Koordinaten des Punktes an, in dem sich die beiden Geraden schneiden.
| AFB II | Kompetenzen K4 K5 | Bearbeitungszeit 11 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 11 Geradenbüschel 𝕃
Im obigen Koordinatensystem sind verschiedene Geraden eingezeichnet.
- Nenne eine Gemeinsamkeit aller dieser Geraden.
- Gib zu drei dieser Geraden die zugehörige Gleichung an.
- Gib an, wie die Gleichung der Parallelen zur x-Achse bzw. zur y-Achse in diesem Bündel lautet.
- Beurteile, welche der beiden Gleichungen aus c) keine Funktion beschreibt.
| AFB II | Kompetenzen K1 K4 K5 K6 | Bearbeitungszeit 11 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 11 Onlinespiel-Kosten
Der Anbieter eines Onlinespiels wirbt für folgenden Spieltarif
| Die ersten 6 Minuten für 4 Cent je Minute spielen, danach für 2 Cent je Minute. |
a) Überprüfe, welche der nachfolgenden Wertetabellen diesen Tarif beschreibt.
Tabelle 1
| Zeit (in Minuten) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Gesamtkosten (in Cent) | 4 | 4 | 4 | 4 | 4 | 4 | 2 | 2 | 2 | 2 |
Tabelle 2
| Zeit (in Minuten) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Gesamtkosten (in Cent) | 4 | 8 | 12 | 16 | 20 | 24 | 26 | 28 | 30 | 32 |
Tabelle 3
| Zeit (in Minuten) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Gesamtkosten (in Cent) | 4 | 8 | 12 | 16 | 20 | 24 | 38 | 40 | 42 | 44 |
Richtig ist Tabelle .
Ein Konkurrent wirbt hingegen für folgenden Tarif
| Die ersten 10 Minuten für 5 Cent je Minute spielen, danach für 2 Cent je Minute. |
b) Erstelle eine Wertetabelle für die ersten 20 Spielminuten dieses Spieltarifs.
c) Zeichne ein Schaubild, das die Kosten in Cent in Abhängigkeit von den gespielten Minuten darstellt.
| AFB II | Kompetenzen K3 K4 K5 | Bearbeitungszeit 16 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 11 Paddelboottour 𝕃
Lisa und ihre Eltern möchten im Spreewald eine Paddelboottour machen.
Sie stehen folgender Informationstafel gegenüber:
Leihgebühr 7,00 € + jede Minute 0,10 €
Keine Leihgebühr, jede Minute kostet 0,30 €
Pauschalpreis für 90 Minuten 15,00 €.
Jede darüber hinausgehende Minute kostet 0,50 €.
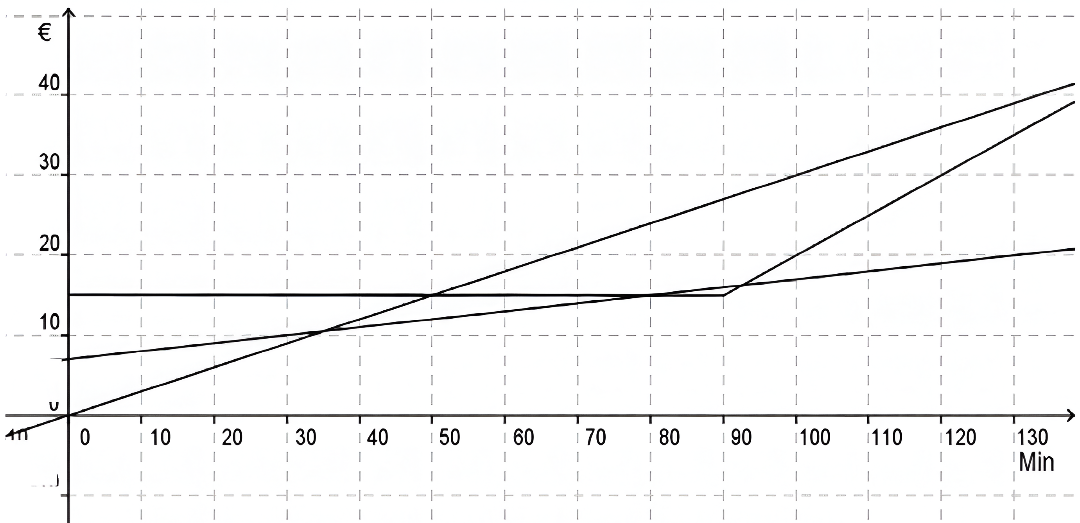
- Ordne die Schaubilder den Angeboten zu.
- Bestimme, welches Angebot die Familie nutzen soll, wenn die Familienmitglieder 30 Minuten fahren, dafür aber möglichst wenig ausgeben möchten.
- Der Vater ist bereit, 25,00 € für die Paddelboottour auszugeben.
Ermittle das Angebot, mit dem Familie möglichst lange fahren kann.
Berechne, wie lange sie bei diesem Angebot fahren können. - Beurteile, ob es eine Fahrtdauer gibt, bei der es egal ist, welches Angebot gewählt wird.
| AFB II | Kompetenzen K1 K3 K4 K5K6 | Bearbeitungszeit 17 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 11 Handytarife Schaubildern zuordnen 𝕃
a) Ordne den folgenden Tarifen je ein Schaubild zu
Keine Grundgebühr und ganztags nur 0,50 €/Min. in alle Netze!
Superflat für 25,00 €!
Grundgebühr 10 €, ganztags 0,30 €/Min. in alle Netze! Die ersten 50 Minuten sind inklusive!
Grundgebühr 10 €, ganztags 0,30 €/Min. in alle Netze!
Grundgebühr 20 €, ganztags 0,20 €/Min. in alle Netze!
b) Gib die Geradengleichungen zu den einzelnen Handytarifen an.
| AFB II | Kompetenzen K3 K4 K5 | Bearbeitungszeit 9 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 11 Akkuentladung 𝕃
Kevin hat ein Handy mit einem Akku, der sich im Ruhezustand innerhalb von 14 Tagen gleichmäßig entleert. Wenn der Akku voll geladen ist, enthält er 200 mAh elektrische Ladung.
- Stelle die Entladung des Akkus in 14 Tagen in einem Schaubild dar.
- Bestimme, wie viel Ladung der Akku nach 9 Tagen enthält.
- Berechne, nach wie vielen Tagen 80 Prozent der Ladung weg sind.
| AFB II | Kompetenzen K3 K4 K5 | Bearbeitungszeit 9 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 11 Richtig-Falsch-Aufgabe zu Schaubildern linearer Funktionen 𝕃
Kreuze jeweils an, ob die Aussage richtig oder falsch ist.
Formuliere die falschen Aussagen zu einer richtigen Aussage um.
- Gerade a hat die Steigung \(\frac{1}{3}\).
☐ richtig ☐ falsch - Der y-Achsenabschnitt der Geraden c beträgt 3,5.
☐ richtig ☐ falsch - Die Gerade b hat die Steigung 1.
☐ richtig ☐ falsch - Die Geraden a und b schneiden sich im Punkt \(S\left(-\frac{33}{8}\Bigl|\frac{17}{8}\right)\)
☐ richtig ☐ falsch - Die Geraden c und e schneiden sich nie.
☐ richtig ☐ falsch - Die Gerade e hat die Gleichung \(y=3\).
☐ richtig ☐ falsch - Die Gerade d ist das Schaubild einer Funktion, da jedem x-Wert genau ein y-Wert zugeordnet wird.
☐ richtig ☐ falsch - Die Geraden b und e schneiden sich im Punkt \(S(3|-5,5)\)
☐ richtig ☐ falsch - Die Geraden a und f unterscheiden sich nur durch ihren y-Achsenabschnitt.
☐ richtig ☐ falsch - Eine Gerade, die orthogonal (senkrecht) auf der Geraden c stehen würde, hätte die Steigung \(\frac{1}{3}\).
☐ richtig ☐ falsch
| AFB II | Kompetenzen K4 K5 K6 | Bearbeitungszeit 10 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 11 Selbst Beispiele geben 𝕃
Betrachte die Funktion f mit \(f(x)=-\frac{1}{4}x+1\)
- Überprüfe, ob der Punkt \(P(2|0,5)\) auf dem Schaubild liegt.
- Gib je einen Punkt an, der oberhalb bzw. unterhalb der Geraden liegt.
- Gib eine lineare Funktion g an, deren zugehöriges Schaubild das Schaubild von f nicht schneidet.
- Gib eine lineare Funktion h an, deren Schaubild das Schaubild von f im Punkt \(P(1|0,75)\) schneidet.
| AFB II | Kompetenzen K3 K4 K5 | Bearbeitungszeit 10 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 11 Geradengleichungen 𝕃
Gegeben sind die Gerade \(g_1: y=-2x+4\) sowie die Punkte \(A(1|2)\) und \(B(4|3)\).
- Zeige, dass der Punkt A auf der Geraden g1 liegt.
- Bestimme die Gleichung einer Geraden g2 durch die Punkte \(A(1|2)\) und \(B(4|3)\).
- Berechne die Koordinaten des Schnittpunkts von g1 und g2. Gib an, welcher Punkt sich dabei ergeben muss.
| AFB II | Kompetenzen K5 | Bearbeitungszeit 10 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 11 Zusammenhang Masse und Volumen 𝕃
Vergleicht man Stoffe mit dem gleichen Volumen, so besitzen diese meist unterschiedliche Massen. Der Zusammenhang zwischen Masse und Volumen für verschiedene Stoffe wird in folgendem Diagramm dargestellt:
- Die Stoffe besitzen jeweils ein Volumen von 300 cm3. Bestimme die Masse des jeweiligen Stoffs.
- Berechne, bei welchem Volumen Magnesium die gleiche Masse besitzt wie 300 cm3 Wasser.
- Bestimme jeweils eine zugehörige Geradengleichung.
| AFB II | Kompetenzen K4 K5 | Bearbeitungszeit 10 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 11 Orthogonale Geraden 𝕃
Gegeben sind die Gerade \( g_1 : y = \frac{3}{4}x + 2\) sowie der Punkt \(A(7|1)\).
- Zeichne die Gerade \(g_1\) und den Punkt \(A\) in ein Koordinatensystem.
- Bestimme die Gleichung einer zu \(g_1\) orthogonalen (rechtwinkligen) Geraden \(g_2\) durch den Punkt \(A\).
Zeichne \(g_2\) in das Koordinatensystem ein. - Berechne die Koordinaten des Schnittpunkts \(S\) von \(g_1\) und \(g_2\).
- Berechne den Abstand der Punkte \(A\) und \(S\).
- Beschreibe, welche Bedeutung dieser Abstand für die Gerade \(g_1\) und den Punkt \(A\) hat.
| AFB II | Kompetenzen K1 K4 K5 K6 | Bearbeitungszeit 15 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 11 Die Temperatur in den USA 𝕃
Antons Freund aus den USA berichtet per Email, wie warm es ist. Da gibt es Temperaturen von 84°, 96°. Anton wundert sich zunächst und erfährt dann, dass in USA die Temperatur nicht nach Celsius (°C) sondern nach Fahrenheit (°F) gemessen werden. Der Zusammenhang zwischen der Celsius- und der Fahrenheitskala ist linear; 0°C sind 32°F, 100°C sind 212° F.
Anton möchte für sich ein Diagramm erstellen, um die Angaben seines Freundes in Grad Celsius umzuwandeln.
- Erstelle eine solches Diagramm und stelle eine Umrechnungsformel auf.
- Beurteile, was für die Verwendung der Fahrenheit-Skala spricht.
| AFB II | Kompetenzen K1 K3 K4 K5 K6 | Bearbeitungszeit 12 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
BPE 4.1 Lineares Gleichungssystem, Lösung und Lösbarkeit
Aufgabe 12 LGS mit drei Variablen 𝕃
Drei Tanten Karin, Brigitte und Jutta werden nach ihrem Alter gefragt. Da alle drei Tanten ihr Alter ungern einfach preisgeben, antworten sie: ohne Karin sind wir 130 Jahre alt, ohne Brigitte sind es 124 Jahre und ohne Jutta sind es 122 Jahre. Berechne das Alter von Karin, Brigitte und Jutta.
| AFB II | Kompetenzen K4 K5 K6 | Bearbeitungszeit 15 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 12 Drinks auf dem Schulfest 𝕃
Tom und Tina trinken auf einem Schulfest über den Tag verteilt mehrere alkoholfreie Cocktails. Tom trinkt dabei fünf Pina Colada, Tina hingegen nur zwei. Vom Cocktail Zombi trinkt Tom vier und Tina drei.
Zu Beginn des Schulfestes hatte Tom 10€ im Geldbeutel, als er es verlässt, sind es nur noch 4,30€.
Tina hat für ihre Getränke 3,40€ bezahlt.
Berechne, wie viel Euro je ein Cocktail der beiden Sorten gekostet hat.
| AFB II | Kompetenzen K1 K3 K5 K6 | Bearbeitungszeit 10 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
BPE 5.1 Ortslinien und Geometrie im Dreieck
Aufgabe 14 Seitenhalbierende im Dreieck 𝕃
Die Seitenhalbierenden in einem Dreieck verbinden jeweils eine Ecke des Dreiecks mit der Mitte der gegenüberliegenden Seite.
Ein Dreieck im Koordinatensystem hat die Eckpunkte \(A(-1|-2), B(5|3)\) und \(C(3|7)\).
- Bestimme die Gleichung der Gerade, die durch \(A\) und durch den Mittelpunkt der Strecke \(BC\) geht. Überprüfe dein Ergebnis in einem Schaubild.
- Bestimme die Gleichung der Gerade, die durch den Punkt \(B\) und durch den Mittelpunkt der Strecke \(AC\) geht. Überprüfe dein Ergebnis im Schaubild.
- Der Schnittpunkt der Geraden (Seitenhalbierenden) ist der Schwerpunkt des Dreiecks. Berechne die Koordinaten dieses Schwerpunkts.
| AFB II | Kompetenzen K4 K5 | Bearbeitungszeit 10 min |
| Quelle Team Mathebrücke | Lizenz k.A. | |
Klasse 9
BPE 7.2 Quadratische Gleichungen
Aufgabe 5 Wo ist der Fehler? 𝕃
Wo ist der Fehler?
| AFB II | Kompetenzen K5 | Bearbeitungszeit 2 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 5 Entscheiden für den effektiven Lösungsweg 𝕃
- Kreuze bei den nachfolgenden Aufgaben an, welcher Rechenweg der effektivste ist.
| abc-Formel bzw. pq-Formel | Ausklammern und Satz vom Nullprodukt | \(x^2\) isolieren und Wurzel ziehen | ||
| a) | \(x^2 + 2x - 3 = 0\) | |||
| b) | \(4x^2 - 3 = 5\) | |||
| c) | \(2x^2 - x = 0\) | |||
| d) | \(5x - 14 = -x^2\) | |||
| e) | \(4x^2 = x^2\) | |||
| f) | \(2x - 8x^2 = -3\) | |||
| g) | \(4x(x - 3) = 0\) | |||
| h) | \((x - 3)4x = 7\) |
- Bestimme jeweils die Lösungsmenge in \(G=\mathbb{R}\).
| AFB II | Kompetenzen k.A. | Bearbeitungszeit k.A. |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
BPE 8.3 Eigenschaften
Aufgabe 9 Nullstellen 𝕃
Begründe, welche der folgenden Behauptungen wahr oder falsch sind.
- Eine nach oben geöffnete Parabel mit dem Scheitelpunkt P(3|4) schneidet die x-Achse nicht.
- Eine nach unten geöffnete Parabel mit dem Scheitelpunkt P(15|30) schneidet die x-Achse zwei Mal.
| AFB II | Kompetenzen K1 | Bearbeitungszeit 5 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 9 Wertetabelle 𝕃
Gegeben ist die folgende Wertetabelle einer Parabel:
| \(x\) | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| \(y\) | 11 | 3 | 2 | 3 | 6 |
- Vervollständige die Wertetabelle.
- Bestimme den Scheitelpunkt der Parabel.
- Gib zwei Eigenschaften der Parabel an.
| AFB II | Kompetenzen K4 K5 K6 | Bearbeitungszeit 8 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 10 Abschnittsweise definierte Funktionen 𝕃

- Lies folgende Funktionswerte ab:
\(f(0) = \)
\(f(3,5) = \)
\(f(-1) = \)
\(f(2) = \) - An welchen Stellen gilt \(y = 4\)?
- Gib die zugehörigen Gleichungen der Funktion an.
| AFB II | Kompetenzen K4 K5 | Bearbeitungszeit 4 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 11 Schnittpunktberechnung überprüfen 𝕃
Ein Schüler hat die gegenseitige Lage einer Parabel p und einer Geraden g bestimmt. Überprüfe sein Ergebnis.
\(x_{1/2} = \frac{6}{2} \pm \sqrt{\left(\frac{6}{2}\right)^2 - 9} \ \Rightarrow \text{Die Gerade schneidet die Parabel nicht}.\)
| AFB II | Kompetenzen K1 K4 K5 | Bearbeitungszeit 6 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 11 Gerade verschieben 𝕋 𝕃
Verschiebe die abgebildete Gerade so, dass sie
- die Parabel schneidet
- die Parabel berührt
- mit der Parabel keinen Punkt gemeinsam hat.
Nenne für jeden der drei Fälle eine Gleichung einer Geraden.
| AFB II | Kompetenzen K2 K3 K5 | Bearbeitungszeit 10 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 13 Rechteck – Fläche - Umfang 𝕃
Gibt es ein Rechteck mit dem Umfang 10 cm und dem Flächeninhalt 4 cm2?
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB II | Kompetenzen K2 K3 K4 K5 | Bearbeitungszeit 8 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 14 Schnitt von Parabel und Gerade 𝕃
Untersuche, wie Parabel und Gerade zueinander liegen. Ermittle, falls vorhanden, die Koordinaten der gemeinsamen Punkte.
- \(y=6x^2; \quad y=5x+4\)
- \(y=2x^2-\frac{3}{2}; \quad y=3\)
- \(y=x^2; \quad y=3x-4\)
- \(y=x^2-3; \quad y=2x-4\)
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB II | Kompetenzen K5 | Bearbeitungszeit 20 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 14 Verlauf einer Parabel 𝕃
Die folgenden Gleichungen gehören zu den Abbildungen 1 bis 3:
| \(\text{(I)} \ y=-x^2-3x+2\) | \(\text{(II)} \ y=3x^2+6x-3\) | \(\text{(III)} \ y=x^2-4x+1\) |
| Abb.1 | Abb.2 | Abb.3 |
- Gib an, zu welchem Schaubild die jeweilige Gleichung gehört und begründe deine Antwort durch Angabe einer Eigenschaft.
- Welche der Parabeln wird von der Geraden \(g\) mit \(y=x-6\) geschnitten? Begründe ohne weitere Rechnung.
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB II | Kompetenzen K5 K6 | Bearbeitungszeit 5 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 14 Zahnparabel 𝕃
Das Bild zeigt das Gipsmodell eines Oberkiefers. Der Zahnarzt hat es angefertigt, um Füllungen für die Löcher herzustellen. Vier Zähne sind durch Karies geschädigt.
Julia sagt: „Die Zahnreihe bildet eine perfekte Parabel.“
Was meinst du?
Hat der Mensch eine Parabel im Mund?
Wenn du das Bild auf Papier gedruckt hast, kannst du versuchen eine passende Parabel über die Zahnreihe zu legen.
Du kannst auch einen Abdruck deiner eigenen Zahnreihe auf ein Papierstück
„beißen“ und versuchen eine passende Parabel zu finden.
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB II | Kompetenzen K2 K3 K5 | Bearbeitungszeit 7 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 14 Parabelscharen 1 𝕃
Eine Düse am Boden spritzt einen Wasserstrahl im Winkel von 45° gegen die Waagerechte. Der Wasserstrahl ist parabelförmig gebogen. Je nach Wasserdruck ergeben sich kleine oder große Bögen.
\(f_t(x)=-\frac{1}{t}\cdot x^2+x\) beschreibt die Schar der möglichen Parabeln. (\(t>0\))
Setze für t den Wert 1 ein und zeichne die Parabel.
Setze für t den Wert 2 ein und zeichne die Parabel.
Setze für t den Wert 3 ein und zeichne die Parabel.
....
Was fällt auf? Was haben alle Parabeln gemeinsam?
Was ändert sich, wenn man t ändert?
Wo trifft der Strahl wieder auf den Boden? Kann man das allgemein für alle Werte von t sagen?
Info: \(x\) ist die Funktionsvariable, \(t\) ist der „Schar-Parameter“ .
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB II | Kompetenzen k.A. | Bearbeitungszeit k.A. |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 14 Parabelscharen 2 𝕃
\(f_t(x) = x^2 -2t\cdot x +t^2\) beschreibt eine Schar von Parabeln.
Setze für \(t\) verschiedene Werte ein und zeichne die Parabeln.
Beschreibe Gemeinsamkeiten und Unterschiede.
Wo liegen die Scheitel der Parabeln?
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB II | Kompetenzen k.A. | Bearbeitungszeit k.A. |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 14 Parabelscharen 3 𝕃
\(f_t(x) = x^2 -2t\cdot x\) beschreibt eine Schar von Parabeln.
Setze für \(t\) verschiedene Werte ein und zeichne die Parabeln.
Beschreibe Gemeinsamkeiten und Unterschiede.
Gib die Schnittpunkte mit der x-Achse und den x-Wert des Scheitels an - zuerst für einzelne Werte von \(t\) dann allgemein.
Zeichne zusätzlich die Parabel \(y = -x^2\) . Was fällt auf?
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB II | Kompetenzen k.A. | Bearbeitungszeit k.A. |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 14 Parabelscharen 4 𝕃
\(f_t(x) = x^2 -2t\cdot x+t^2+\frac{1}{2}t\) beschreibt eine Schar von Parabeln.
Wo liegen die Scheitel der Parabeln?
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB II | Kompetenzen k.A. | Bearbeitungszeit k.A. |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
BPE 9.1 Rechtwinkliges Dreieck, Satz des Pythagoras
Aufgabe 15 Umfang eines Dreiecks 𝕃
Berechne den Umfang des Dreiecks \(ABC\) mit \(A(-2|3), B(10|-2), C(1|7)\).
| AFB II | Kompetenzen K5 | Bearbeitungszeit 5 min |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Klasse 10
BPE 14 Einheitsübergreifend
Aufgabe 20 Bakterienwachstum 2 𝕃
E-Coli-Bakterien verdoppeln ihre Anzahl alle 20 Minuten.
Wir nehmen an, dass am Anfang 100 Bakterien vorhanden sind.
Beschreibe, wie sich die Bakterienzahl dann in den ersten 2 Stunden entwickelt.
Zeichne das Schaubild der Entwicklung in ein geeignetes Koordinatensystem.
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB II | Kompetenzen k.A. | Bearbeitungszeit k.A. |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 20 Bakterienwachstum 3 𝕃
E-Coli-Bakterien verdoppeln ihre Anzahl alle 20 Minuten.
Wir nehmen an, dass am Anfang 100 Bakterien vorhanden sind.
Beschreibe, wie sich die Bakterienzahl dann in den ersten 2 Stunden entwickelt.
- Stelle die Entwicklung für diesen Zeitraum mithilfe einer Wertetafel dar.
- Die Entwicklung wird mithilfe einer Funktion beschrieben. Bestimme einen Funktionsterm.
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB II | Kompetenzen k.A. | Bearbeitungszeit k.A. |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
Aufgabe 20 Bakterienwachstum 4 𝕃
E-Coli-Bakterien verdoppeln ihre Anzahl alle 20 Minuten.
Wir nehmen an, dass am Anfang 100 Bakterien vorhanden sind.
Beschreibe, wie sich die Bakterienzahl dann in den ersten 2 Stunden entwickelt.
- Stelle die Entwicklung für diesen Zeitraum mithilfe einer Wertetafel dar.
- Beurteile, wie viele Bakterien nach 10 Minuten vorhanden sind.
1) 150 2) weniger als 150 3) mehr als 150
Inhalt für Lehrende (Anmeldung erforderlich)
| AFB II | Kompetenzen k.A. | Bearbeitungszeit k.A. |
| Quelle Team Mathebrücke | Lizenz CC BY-SA | |
