BPE 12.2 Ableitungsfunktion und Ableiten
K4 Ich kann ausgehend vom grafischen Differenzieren, Ableitungen für ausgewählte Funktionen bestimmen
K1 K6 Ich kann die Bedeutung der Eulerschen Zahl e als besondere Basis bei Exponentialfunktionen zur Berechnung ihrer Ableitung nennen
K1 K6 Ich kann den Zusammenhang von trigonometrischen Funktionen mit ihren Ableitungsfunktionen beschreiben
1 eFunktion (k.A.) 𝕃
Zeichne die e-Funktion \(f(x)=e^x\) im Intervall \([-1;3]\). Zeichne genau darunter ein Koordinatensystem mit der Ableitungsfunktion \(f'(x)\), deren Werte durch grafisches Differenzieren an mindestens 5 Stellen ermittelt werden. Beschreibe dein Ergebnis und finde eine Lösung für den Term der Ableitungsfunktion.
| AFB k.A. - k.A. | Quelle k.A. |
2 Trigonometrische Funktionen (k.A.) 𝕋 𝕃
Zeichne die sinus-Funktion \(f(x)=sin(x)\) im Intervall \([-2 /pi;2 /pi]\). Zeichne genau darunter ein Koordinatensystem mit der Ableitungsfunktion \(f'(x)\), deren Werte durch geschicktes grafisches Differenzieren ermittelt werden. Beschreibe dein Ergebnis und finde eine Lösung für den Term der Ableitungsfunktion.
Was gilt analog für \(f(x)=cos(x)\), \(f(x)=-sin(x)\) und \(f(x)=-cos(x)\)?
| AFB k.A. - k.A. | Quelle k.A. |
3 Verschiebung durch Ableiten (k.A.)
Die in \(\mathbb{R}\) definierte Funktion \(f\) hat die erste Ableitungsfunktion \(f^\prime\) mit \(f^\prime\left(x\right)=2\cdot e^{2x}\) und es gilt \(f\left(0\right)=1\).
Leitet man die erste Ableitungsfunktion \(f^\prime\) ab, so erhält man die zweite Ableitungsfunktion \(f^{\prime\prime}\) von \(f\). Entsprechend entsteht die hundertste Ableitung \(f^{\left(100\right)}\) von \(f\). Der Graph der hundersten Ableitungsfunktion \(f^{\left(100\right)}\) lässt sich aus dem Graphen von \(f\) durch eine Verschiebung in x-Richtung erzeugen.
Ermittle, um wie viele Einheiten der Graph von \(f\) dazu in x-Richtung zu verschieben ist.
| AFB 3 - K1 K2 K4 K5 | Quelle IQB e.V. | #iqb |
4 Ableitung berechnen und grafisch ermitteln (k.A.) 𝕋 𝕃
Gegeben sind die in \(\mathbb{R}\) definierten Funktionen \(g\) mit \(g\left(x\right)=2\cdot e^x-2\) und \(h\) mit \(h\left(x\right)=e^x+1\). Die Abbildung zeigt ihre Graphen.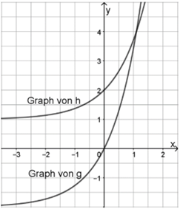
- Die erste Ableitungsfunktion von \(g\) wird mit \(g^\prime\) bezeichnet. Berechne \(g^\prime\left(0\right)\) und veranschauliche in der Abbildung, wie man diesen Wert grafisch ermitteln kann.
- Beurteile folgende Aussage:
Es gibt eine Verschiebung in y-Richtung, durch die der Graph von \(h\) aus dem Graphen von \(g\) erzeugt werden kann.
| AFB k.A. - K1 K2 K4 K5 K6 | Quelle IQB e.V. | #iqb |
