BPE 3 Einheitsübergreifend
1 Wertetabellen prüfen (10 min) 𝕃
Beurteile, ob folgende Zuordnungen eine lineare Funktion darstellen. Begründe deine Antwort.
Zusatz (aus BPE 3.5): Gib – wenn möglich – die Funktionsgleichung an.
\(x\) 0 1 2 3 4 5 \(f(x)\) 1,5 3 4,5 6 7,5 9 \(x\) -2 -1 0 1 2 3 \(g(x)\) 4,5 2 -0,5 -3 -5,5 -8 \(x\) 0 3 4 10 12 13 \(h(x)\) 2,5 7 8,5 17,5 20,5 22 \(x\) 0 2 4 6 8 10 \(i(x)\) 0 4 16 36 64 100 \(x\) 0 1 4 6 8 11 \(j(x)\) 40 35 20 10 0 -15 \(x\) -2 0 1 3 7 15 \(k(x)\) 1 0 -0,5 -1,5 -3,5 -7,5 \(x\) -4 -1 1 3 6 7 \(l(x)\) 69 3 9 55 199 267
| AFB II - K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
2 Schnittpunkt zweier Geraden (15 min) 𝕃
 Die Abbildung zeigt zwei Geraden, die sich schneiden.
Die Abbildung zeigt zwei Geraden, die sich schneiden.
- Lies den Schnittpunkt aus der Abbildung möglichst genau ab.
- Ermittle die Geradengleichungen.
- Berechnen den Schnittpunkt exakt.
- Vergleiche die Ergebnisse aus a) und c).
| AFB II - K4 K5 K6 | Quelle kickoff |
3 Zuordnungsaufgabe Funktionsterm und Schaubild (7 min) 𝕃
Ordne den Schaubildern zu:
a) \(y=-\frac{3}{4}x+2\) b) \(y=\frac{1}{3}x\) c) \(y=-\frac{4}{3}x+2\) d) \(y=3x\)
1)  | 2) |
3)  | 4)  |
| AFB II - K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
4 Geradengleichungen bestimmen (11 min) 𝕃
- Bestimme die Gleichungen der beiden Geraden.
- Bestimme die Schnittpunkte der beiden Geraden mit der x-Achse.
- Gib die Koordinaten des Punktes an, in dem sich die beiden Geraden schneiden.
| AFB II - K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
5 Einkommenssteuer 2025 (10 min)
Beträgt das zu versteuernde Jahreseinkommen mehr als 68 480 € und weniger als 277 826 €, wird die Einkommensteuer (in Euro) berechnet nach der Vorschrift
\( 0,42\cdot x\ –\ 10\ 912\).
Dabei ist \(x\) das zu versteuernde Einkommen.
- Berechne, wie viel Einkommensteuer (in Euro) man bezahlt, wenn das Einkommen 72 882 € beträgt.
- Berechne, wie viel Prozent des Einkommens das sind.
- Berechne, wie viel Steuer man mehr zahlen muss, wenn das Einkommen 100 € höher ist.
Gib an, wieviel Prozent von den 100 € Mehreinkommen das sind.
Zusatz: (Evtl. Potenzfunktionen mit negativen Exponenten erforderlich)
Begründe, warum der in b) berechnete Prozentsatz bei steigendem Einkommen größer wird.
| AFB I - K1 K5 K6 | Quelle Team Mathebrücke | #mathebrücke |
6 Geradenbüschel (11 min) 𝕃
Im obigen Koordinatensystem sind verschiedene Geraden eingezeichnet.
- Nenne eine Gemeinsamkeit aller dieser Geraden.
- Gib zu drei dieser Geraden die zugehörige Gleichung an.
- Gib an, wie die Gleichung der Parallelen zur x-Achse bzw. zur y-Achse in diesem Bündel lautet.
- Beurteile, welche der beiden Gleichungen aus c) keine Funktion beschreibt.
| AFB II - K1 K4 K5 K6 | Quelle Team Mathebrücke | #mathebrücke |
7 Onlinespiel-Kosten (16 min)
Der Anbieter eines Onlinespiels wirbt für folgenden Spieltarif
| Die ersten 6 Minuten für 4 Cent je Minute spielen, danach für 2 Cent je Minute. |
a) Überprüfe, welche der nachfolgenden Wertetabellen diesen Tarif beschreibt.
Tabelle 1
| Zeit (in Minuten) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Gesamtkosten (in Cent) | 4 | 4 | 4 | 4 | 4 | 4 | 2 | 2 | 2 | 2 |
Tabelle 2
| Zeit (in Minuten) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Gesamtkosten (in Cent) | 4 | 8 | 12 | 16 | 20 | 24 | 26 | 28 | 30 | 32 |
Tabelle 3
| Zeit (in Minuten) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Gesamtkosten (in Cent) | 4 | 8 | 12 | 16 | 20 | 24 | 38 | 40 | 42 | 44 |
Richtig ist Tabelle .
Ein Konkurrent wirbt hingegen für folgenden Tarif
| Die ersten 10 Minuten für 5 Cent je Minute spielen, danach für 2 Cent je Minute. |
b) Erstelle eine Wertetabelle für die ersten 20 Spielminuten dieses Spieltarifs.
c) Zeichne ein Schaubild, das die Kosten in Cent in Abhängigkeit von den gespielten Minuten darstellt.
| AFB II - K3 K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
8 Paddelboottour (17 min) 𝕃
Lisa und ihre Eltern möchten im Spreewald eine Paddelboottour machen.
Sie stehen folgender Informationstafel gegenüber:
Leihgebühr 7,00 € + jede Minute 0,10 €
Keine Leihgebühr, jede Minute kostet 0,30 €
Pauschalpreis für 90 Minuten 15,00 €.
Jede darüber hinausgehende Minute kostet 0,50 €.
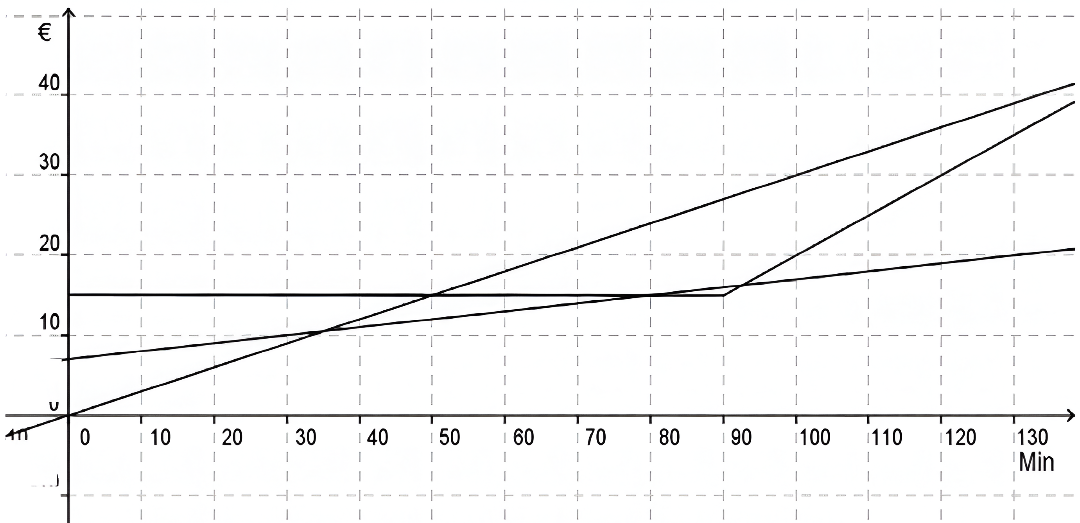
- Ordne die Schaubilder den Angeboten zu.
- Bestimme, welches Angebot die Familie nutzen soll, wenn die Familienmitglieder 30 Minuten fahren, dafür aber möglichst wenig ausgeben möchten.
- Der Vater ist bereit, 25,00 € für die Paddelboottour auszugeben.
Ermittle das Angebot, mit dem Familie möglichst lange fahren kann.
Berechne, wie lange sie bei diesem Angebot fahren können. - Beurteile, ob es eine Fahrtdauer gibt, bei der es egal ist, welches Angebot gewählt wird.
| AFB II - K1 K3 K4 K5K6 | Quelle Team Mathebrücke | #mathebrücke |
9 Handytarife Schaubildern zuordnen (9 min) 𝕃
a) Ordne den folgenden Tarifen je ein Schaubild zu
Keine Grundgebühr und ganztags nur 0,50 €/Min. in alle Netze!
Superflat für 25,00 €!
Grundgebühr 10 €, ganztags 0,30 €/Min. in alle Netze! Die ersten 50 Minuten sind inklusive!
Grundgebühr 10 €, ganztags 0,30 €/Min. in alle Netze!
Grundgebühr 20 €, ganztags 0,20 €/Min. in alle Netze!
b) Gib die Geradengleichungen zu den einzelnen Handytarifen an.
| AFB II - K3 K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
10 Akkuentladung (9 min) 𝕃
Kevin hat ein Handy mit einem Akku, der sich im Ruhezustand innerhalb von 14 Tagen gleichmäßig entleert. Wenn der Akku voll geladen ist, enthält er 200 mAh elektrische Ladung.
- Stelle die Entladung des Akkus in 14 Tagen in einem Schaubild dar.
- Bestimme, wie viel Ladung der Akku nach 9 Tagen enthält.
- Berechne, nach wie vielen Tagen 80 Prozent der Ladung weg sind.
| AFB II - K3 K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
11 Richtig-Falsch-Aufgabe zu Schaubildern linearer Funktionen (10 min) 𝕃
Kreuze jeweils an, ob die Aussage richtig oder falsch ist.
Formuliere die falschen Aussagen zu einer richtigen Aussage um.
- Gerade a hat die Steigung \(\frac{1}{3}\).
☐ richtig ☐ falsch - Der y-Achsenabschnitt der Geraden c beträgt 3,5.
☐ richtig ☐ falsch - Die Gerade b hat die Steigung 1.
☐ richtig ☐ falsch - Die Geraden a und b schneiden sich im Punkt \(S\left(-\frac{33}{8}\Bigl|\frac{17}{8}\right)\)
☐ richtig ☐ falsch - Die Geraden c und e schneiden sich nie.
☐ richtig ☐ falsch - Die Gerade e hat die Gleichung \(y=3\).
☐ richtig ☐ falsch - Die Gerade d ist das Schaubild einer Funktion, da jedem x-Wert genau ein y-Wert zugeordnet wird.
☐ richtig ☐ falsch - Die Geraden b und e schneiden sich im Punkt \(S(3|-5,5)\)
☐ richtig ☐ falsch - Die Geraden a und f unterscheiden sich nur durch ihren y-Achsenabschnitt.
☐ richtig ☐ falsch - Eine Gerade, die orthogonal (senkrecht) auf der Geraden c stehen würde, hätte die Steigung \(\frac{1}{3}\).
☐ richtig ☐ falsch
| AFB II - K4 K5 K6 | Quelle Team Mathebrücke | #mathebrücke |
12 Selbst Beispiele geben (10 min) 𝕃
Betrachte die Funktion f mit \(f(x)=-\frac{1}{4}x+1\)
- Überprüfe, ob der Punkt \(P(2|0,5)\) auf dem Schaubild liegt.
- Gib je einen Punkt an, der oberhalb bzw. unterhalb der Geraden liegt.
- Gib eine lineare Funktion g an, deren zugehöriges Schaubild das Schaubild von f nicht schneidet.
- Gib eine lineare Funktion h an, deren Schaubild das Schaubild von f im Punkt \(P(1|0,75)\) schneidet.
| AFB II - K3 K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
13 Geradengleichungen (10 min) 𝕃
Gegeben sind die Gerade \(g_1: y=-2x+4\) sowie die Punkte \(A(1|2)\) und \(B(4|3)\).
- Zeige, dass der Punkt A auf der Geraden g1 liegt.
- Bestimme die Gleichung einer Geraden g2 durch die Punkte \(A(1|2)\) und \(B(4|3)\).
- Berechne die Koordinaten des Schnittpunkts von g1 und g2. Gib an, welcher Punkt sich dabei ergeben muss.
| AFB II - K5 | Quelle Team Mathebrücke | #mathebrücke |
14 Zusammenhang Masse und Volumen (10 min) 𝕃
Vergleicht man Stoffe mit dem gleichen Volumen, so besitzen diese meist unterschiedliche Massen. Der Zusammenhang zwischen Masse und Volumen für verschiedene Stoffe wird in folgendem Diagramm dargestellt:
- Die Stoffe besitzen jeweils ein Volumen von 300 cm3. Bestimme die Masse des jeweiligen Stoffs.
- Berechne, bei welchem Volumen Magnesium die gleiche Masse besitzt wie 300 cm3 Wasser.
- Bestimme jeweils eine zugehörige Geradengleichung.
| AFB II - K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
15 Aufgabe zu Funktionsvorschriften (10 min) 𝕃
Gegeben sind die Funktionen \(f\) mit \(f(x) = \frac{1}{8}x - \frac{3}{2}\) und \(g\) mit \(g(x) = -\frac{1}{2}x + \frac{7}{8}\).
- Bestimme den Wert von \(x\), wenn gilt: \(f(x) = -\frac{5}{8}\)
- Berechne den Wert von \(x\), wenn gilt: \(f(7) = g(x)\)?
- Ermittle den Wert von \(c\), wenn gilt: \(f(5) + c = g(6)\).
| AFB III - K5 | Quelle Team Mathebrücke | #mathebrücke |
16 Richtig-Falsch-Aufgaben zu Funktionsvorschriften (10 min) 𝕃
Gegeben sind die Funktionen \(f\) durch \(f(x) = -3x+7\) und \(g\) durch \(g(x) = \frac{1}{3}x-2\).
Kreuze jeweils an, ob die Aussage richtig oder falsch ist.
Formuliere die falschen Aussagen zu einer richtigen Aussage um.
- Die Funktion \(f\) nimmt an der Stelle 3 den Funktionswert 1 an.
☐ richtig ☐ falsch - Es gilt \(g(9) = 1\).
☐ richtig ☐ falsch - Das Schaubild der Funktion \(f\) schneidet die x-Achse an der Stelle \(\frac{7}{3}\).
☐ richtig ☐ falsch - Die Funktionen \(f\) und \(g\) nehmen an der Stelle \(x = 2,5\) denselben Funktionswert an.
☐ richtig ☐ falsch - Die Schaubilder der Funktionen stehen senkrecht aufeinander.
☐ richtig ☐ falsch - Die Funktion \(f\) ordnet dem Wert 5 eine kleinere Zahl zu als die Funktion \(g\).
☐ richtig ☐ falsch - Die Funktion \(g\) ordnet allen Werten größer 6 negative Funktionswerte zu.
☐ richtig ☐ falsch
| AFB III - K4 K5 K6 | Quelle Team Mathebrücke | #mathebrücke |
17 Länge und Mittelpunkt einer Strecke (10 min) 𝕃
In nachfolgendem Koordinatensystem sind mehrere Punkte eingezeichnet.
- Bestimme die Länge der Strecken \(BE\) und \(BD\).
- Gib die Koordinaten des Mittelpunktes \(M\) der Strecke \(EA\) an.
Überprüfe, ob die Gerade durch den Punkt \(D\) mit Steigung -1 durch \(M\) geht. - Berechne den Umfang des Dreiecks \(BAC\).
| AFB III - K5 | Quelle Team Mathebrücke | #mathebrücke |
18 Länge und Mittelpunkt einer Strecke 2 (8 min) 𝕃
- Berechne die fehlenden Koordinaten, wenn \(M\) der Mittelpunkt der Strecke \(P_1P_2\) ist: \(P_1(-3|2); \ \ P_2(0|0);\ \ M( ?|? )\)
\([P_1(4|?); \ \ P_2(-2|5);\ \ M(?|3,5)] \) - Gegeben sind die Punkte \(A(3|-5)\) und \(B(7|2)\). Bestimme die Gleichung der Geraden mit \(m = 0,5\), die durch den Mittelpunkt der Strecke \(AB\) verläuft.
- Zeige, dass die Entfernung des Punktes \(A\) vom Schnittpunkt der Geraden aus b) mit der y-Achse 10 beträgt.
| AFB III - K5 | Quelle Team Mathebrücke | #mathebrücke |
19 Tinas Orthogonale (8 min) 𝕃
Tina hat folgende Hausaufgabe bekommen: Zwei Geraden stehen orthogonal zueinander und schneiden sich im Punkt \(P(-3|-2)\). Bestimmen Sie mögliche Geradengleichungen.
Schau dir an, was sie in ihr Heft notiert hat:
- Erläutere kurz, warum Tina die Steigung \(m = 5\) frei wählen durfte.
- Bestimme für Tina die zugehörige Orthogonale.
| AFB III - K1 K5 K6 | Quelle Team Mathebrücke | #mathebrücke |
20 T-Shirtkosten (k.A.) 𝕃
Bei der Produktion von T-Shirts mit aufwendigem Druck und aufgenähten Strasssteinen fallen in einem Unternehmen variable Stückkosten (= Kosten für die Produktion eines T-Shirts) in Höhe von 15 Euro an. Ab einer Menge von 200 T-Shirts betragen die variablen Stückkosten nur noch 11 Euro, da das Unternehmen Einkaufsrabatte nutzen kann.
- Bestimme den Funktionsterm, der die Kosten für eine Produktionsmenge kleiner 200 Stück angibt.
Bestimme auch den Funktionsterm für größere Produktionsmengen. - Zeichne den Kostenverlauf des Unternehmens in Abhängigkeit von der Produktionsmenge in ein Koordinatensystem.
- Erläutere, wie sich das Schaubild verändern würde, wenn in dem Unternehmen fixe Kosten, die unabhängig von der produzierten Menge sind, in Höhe von 600 Euro anfallen würden.
| AFB III - K1 K3 K4 K5 K6 | Quelle Team Mathebrücke | #mathebrücke |
21 Fruchtsafttank (10 min) 𝕃
Ein Fruchtsafthersteller nutzt zylinderförmige Edelstahltanks zur Zwischenlagerung von Fruchtsäften. Ein Tank fasst 6000 Liter und wird gleichmäßig gefüllt. Nach 6 Minuten sind 2100 Liter im Tank, eine Viertelstunde später 4350 Liter.
- Stelle die Füllmenge in Abhängigkeit von der Zeit in einem Schaubild dar.
- Bestimme, wie viel Liter zu Beginn noch im Tank waren.
- Berechne, wie lange es dauert, bis der Tank voll ist.
| AFB III - K3 K4 K5 | Quelle Team Mathebrücke | #mathebrücke |
22 Geradenbüschel 2 (8 min) 𝕃
Gegeben ist das nebenstehende "Geradenbüschel" (es sind nur 5 von unendlich vielen Geraden eingezeichnet):
- Beschreibe, was diese Geraden gemeinsam haben.
- Beurteile, welche der folgenden Geraden zum Büschel gehören und welche nicht. Begründe deine Antwort.
| Ja | Nein | |
| \(g_1 : y = -7x + 2\) | ☐ | ☐ |
| \(g_2 : y = 2x - 7\) | ☐ | ☐ |
| \(g_3 : y = 2 - 5x\) | ☐ | ☐ |
| \(g_4 : y = 5 - 2x\) | ☐ | ☐ |
| \(g_5 : y = 2\) | ☐ | ☐ |
| \(g_6 : x = 2\) | ☐ | ☐ |
| \(g_7 : 6x + 3y = 2\) | ☐ | ☐ |
| \(g_8 : 3x + 2y = 4\) | ☐ | ☐ |
| \(g_9 : 2x - 3y = 4\) | ☐ | ☐ |
| AFB III - K4 K5 K6 | Quelle Team Mathebrücke | #mathebrücke |
23 Orthogonale Geraden (15 min) 𝕃
Gegeben sind die Gerade \( g_1 : y = \frac{3}{4}x + 2\) sowie der Punkt \(A(7|1)\).
- Zeichne die Gerade \(g_1\) und den Punkt \(A\) in ein Koordinatensystem.
- Bestimme die Gleichung einer zu \(g_1\) orthogonalen (rechtwinkligen) Geraden \(g_2\) durch den Punkt \(A\).
Zeichne \(g_2\) in das Koordinatensystem ein. - Berechne die Koordinaten des Schnittpunkts \(S\) von \(g_1\) und \(g_2\).
- Berechne den Abstand der Punkte \(A\) und \(S\).
- Beschreibe, welche Bedeutung dieser Abstand für die Gerade \(g_1\) und den Punkt \(A\) hat.
| AFB II - K1 K4 K5 K6 | Quelle Team Mathebrücke | #mathebrücke |
24 Die Temperatur in den USA (12 min) 𝕃
Antons Freund aus den USA berichtet per Email, wie warm es ist. Da gibt es Temperaturen von 84°, 96°. Anton wundert sich zunächst und erfährt dann, dass in USA die Temperatur nicht nach Celsius (°C) sondern nach Fahrenheit (°F) gemessen werden. Der Zusammenhang zwischen der Celsius- und der Fahrenheitskala ist linear; 0°C sind 32°F, 100°C sind 212° F.
Anton möchte für sich ein Diagramm erstellen, um die Angaben seines Freundes in Grad Celsius umzuwandeln.
- Erstelle eine solches Diagramm und stelle eine Umrechnungsformel auf.
- Beurteile, was für die Verwendung der Fahrenheit-Skala spricht.
| AFB II - K1 K3 K4 K5 K6 | Quelle Team Mathebrücke | #mathebrücke |
25 Lösen von linearen Ungleichungen (k.A.) 𝕋 𝕃
Bestimme jeweils grafisch und rechnerisch die Lösungsmenge folgender Ungleichungen:
- \(-2x + 3 < 5\)
- \(3(x + 4) \geq 6\)
- \(5 - 3x > 4(x - 0,5)\)
- \(6 + 3(x - 1) \leq 4(x + 3(x - 1)) - 8x\)
| AFB I - k.A. | Quelle Team Mathebrücke | #mathebrücke |
| K1 | K2 | K3 | K4 | K5 | K6 | |
|---|---|---|---|---|---|---|
| I | 1 | 0 | 0 | 0 | 1 | 1 |
| II | 4 | 0 | 6 | 14 | 15 | 6 |
| III | 2 | 0 | 2 | 4 | 8 | 4 |
