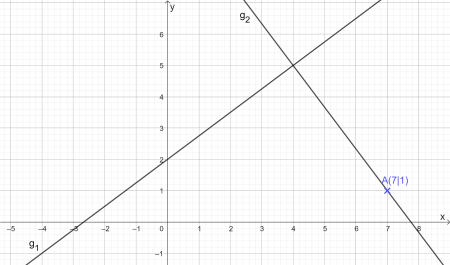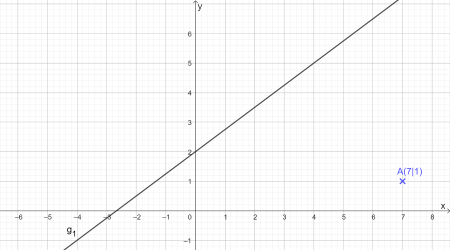
Für die Steigungen zweier orthogonaler Geraden gilt \(m_1\cdot m_2=-1\)
Wir stellen die Gleichung nach \(m_2\) um und berechnen die Steiung von \(g_2\) durch
\(m_2=-\frac{1}{m_1}=--\frac{1}{\frac{3}{4}}=-\frac{4}{3}\).Die Geradengleichung lautet also \(g_2: y=-\frac{4}{3}x+b\)
Um nun den y-Achsenabschnitt \(b\) von \(g_2\) zu berechnen, setzen wir den Punkt \(A(7|1)\) ein und stellen um nach \(b\):
\[\begin{align} 1 =-\frac{4}{3}\cdot 7+b \\ 1 =-\frac{28}{3}+b \quad \mid +\frac{28}{3} \\ b= 1+\frac{28}{3}=\frac{31}{3} \end{align}\]Insgesamt lautet die Geradengleichung damit \(g_2: y=-\frac{4}{3}x+\frac{31}{3}\)