Die Abbildung zeigt den Graphen \(G_f\) der in \(\mathbb{R}\) definierten Funktion \(f: x \mapsto e^{-x}-e^{-2x}\).
\(G_f\) schneidet die x-Achse an der Stelle \(x_1=0\) und hat einen Hochpunkt an der Stelle \(x_H\).
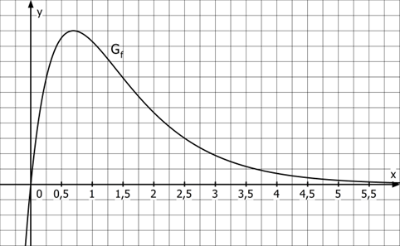
- [2 BE] Weise rechnerisch nach, dass \(x_1\) die einzige Nullstelle von \(f\) ist.
- [3 BE] Entscheide mit Hilfe der Abbildung, ob die folgenden Aussagen wahr oder falsch sind. Begründe jeweils deine Entscheidung.
- \(f^{\prime \prime} (0,5)>0\)
- \(\int_0^2 f(x)dx<2\cdot f(x_H )\)
| Bewertungseinheiten gesamt 5 |
| Aufgabe | BE | Allgemeine mathematische Kompetenzen | Anforderungsbereich |
|---|
| K1 | K2 | K3 | K4 | K5 | K6 | I | II | III |
|---|
| a | 2 | II | | | | I | | 1 | 1 |
|
| b | 3 | II | | | II | | III | | | 3 |
Gegeben ist die Funktion \(f\) mit \(f(x)=(x^2-4)\cdot(x-1)\) mit \(x\in \mathbb{R} \). Ihr Graph ist \(K_f\).
- [1 BE] Gib die Nullstellen von \(f \) an.
- [4 BE] Ermittle eine Gleichung der Tangente an \(K_f\) im Schnittpunkt von \(K_f\) mit der y-Achse.
Zeige, dass diese Tangente mit \(K_f \) einen gemeinsamen Punkt auf der x-Achse hat.
| Bewertungseinheiten gesamt 5 |
| Aufgabe | BE | Allgemeine mathematische Kompetenzen | Anforderungsbereich |
|---|
| K1 | K2 | K3 | K4 | K5 | K6 | I | II | III |
|---|
| a | 1 | I | | | | I | | 1 | |
|
| b | 4 | III | | | III | II | III | | 1 | 3 |
Gegeben sind die beiden 2x2-Matrizen \(A\) und \(B\) sowie der Vektor \(\vec{v}\).
\[A=\left(\begin{matrix}2&-1\\-3&1\\\end{matrix}\right) \ \ \ \ \ \ \ \ \ \ B=\left(\begin{matrix}-1&-1\\-3&-2\\\end{matrix}\right)\ \ \ \ \ \ \ \ \ \ \vec{v}=\left(\begin{matrix}v_1\\v_2\\\end{matrix}\right) \]
- [2 BE] Zeige rechnerisch, dass \(B\) eine inverse Matrix zu \(A\) ist.
- [3 BE] Gib eine mögliche Fragestellung an, die durch die Lösung des folgenden Gleichungssystems beantwortet werden kann.
\[\begin{align}
2v_1-v_2&=1 \\
-3v_1+v_2&=2
\end{align}\]
| Bewertungseinheiten gesamt 5 |
| Aufgabe | BE | Allgemeine mathematische Kompetenzen | Anforderungsbereich |
|---|
| K1 | K2 | K3 | K4 | K5 | K6 | I | II | III |
|---|
| a | 2 | II | | | I | II | | 1 | 1 |
|
| b | 3 | | | | | | III | | | 3 |
Für eine reelle Zahl \(a\) ist die Gerade \(g\) durch \(g: \vec{x}=\left(\begin{matrix}1\\2\\3 \end{matrix}\right)+t\cdot \left(\begin{matrix}1\\1\\a \end{matrix}\right)\) mit \(t\in\mathbb{R}\) gegeben.
Außerdem wird die Ebene \(E\) beschrieben durch \(E: x_1+x_2=3\)
- [2 BE] Bestimme den Wert von \(a\) so, dass sich \(g\) und \(E\) orthogonal schneiden.
- [3 BE] Für \(a=1,5\) schneidet \(g\) die \(x_1\)-Achse im Punkt \(P\) und die Ebene \(E\) im Punkt \(S\left(1\left|2\right|3\right)\). Zudem ist der Punkt \(Q\left(1\left|2\right|0\right)\) bekannt.
Bestimme den Flächeninhalt des Dreiecks \(PQS\).
| Bewertungseinheiten gesamt 5 |
| Aufgabe | BE | Allgemeine mathematische Kompetenzen | Anforderungsbereich |
|---|
| K1 | K2 | K3 | K4 | K5 | K6 | I | II | III |
|---|
| a | 2 | I | | | | II | | 1 | 1 |
|
| b | 3 | | | | III | | II | | | 3 |
[10 BE] Bearbeite die folgende Aufgabe unter Berücksichtigung der einzelnen Problemlöseschritte. Dokumentiere und reflektiere deine Ihre Vorgehensweise.
Drei zufällig mit derselben Wahrscheinlichkeit gewählte, verschiedene Eckpunkte eines regelmäßigen Fünfecks (d. h. alle Seiten sind gleich lang, alle Innenwinkel betragen 108°) werden zu einem Dreieck verbunden.
Untersuche, mit welcher Wahrscheinlichkeit der Mittelpunkt des Fünfecks innerhalb des Dreiecks liegt.
| Bewertungseinheiten gesamt 10 |
| Aufgabe | BE | Allgemeine mathematische Kompetenzen | Anforderungsbereich |
|---|
| K1 | K2 | K3 | K4 | K5 | K6 | I | II | III |
|---|
| 10 | III | III | | II | I | II | 2 | 2 | 6 |

