Teilaufgabe a)
Erwartungshorizont (offiziell)
\(\frac{418,53 - 394,06}{2022 - 2012} = 2,45 \ \left(\mathrm{ppm/Jahr}\right)\)Hinweis: Eine Mittelwertbildung der jährlichen Änderungsraten ist ebenso möglich.
Erläuterung der Lösung
AufgabenstellungBestimme die durchschnittliche Änderungsrate der CO2-Konzentration im Zeitraum 2012 bis 2022.
LösungDie durchschnittliche Änderungsrate ist der gesamte Anstieg der CO2-Konzentration geteilt durch die Dauer des betrachteten Zeitintervalls:
\(\frac{418,53 - 394,06}{2022 - 2012} = 2,45\ \left(\mathrm{ppm/Jahr}\right)\)
Hinweis: Eine Mittelwertbildung der jährlichen Änderungsraten ist ebenso möglich.
Teilaufgabe b)
Erwartungshorizont (offiziell)
Lineare Regression, da z. B. nach dem Einzeichnen der Wertepaare als Punkte in ein Diagramm annähernd eine Gerade zu erkennen ist.\(k(x)=2,48x-4596\)
mit Jahreszahl \(x\) und CO2-Konzentration \(k\) in ppm
Erläuterung der Lösung
AufgabenstellungErmittle ein mathematisches Modell für den gegebenen Verlauf der CO2-Konzentration. Gib dazu eine geeignete Funktionsgleichung an. Begründe deine Auswahl.
LösungLineare Regression, da z. B. nach dem Einzeichnen der Wertepaare als Punkte in ein Diagramm annähernd eine Gerade zu erkennen ist:
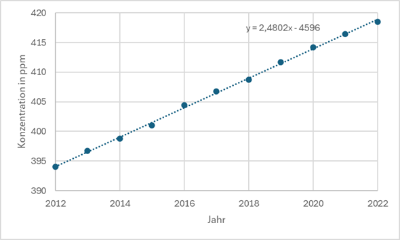
Die Geradengleichung erhält man, indem man eine lineare Regression mit Hilfe des Taschenrechners durchführt:
\(k(x)=2,48x-4596\)
mit Jahreszahl \(x\) und CO2-Konzentration \(k\) in ppm
Ist \(x\) stattdessen die Zeit in Jahren seit 2012 (entspricht \(x=0\)), so ergibt sich: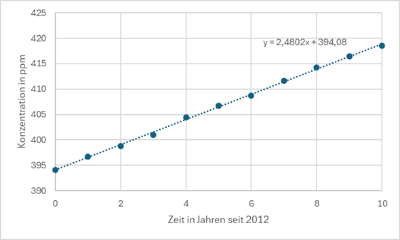
\(k(x)=2,48x+394\)
mit Jahreszahl \(x\) und CO2-Konzentration \(k\) in ppm
Hinweis: Statt einer Regressionsanalyse mit Taschenrechner könnte man hier auch eine Zeichnung anfertigen und per Hand eine Ausgleichsgerade anlegenTeilaufgabe c)
Erwartungshorizont (offiziell)
\(k(2100)=2,48\cdot2100-4596=612\)Laut Modell ist im Jahr 2100 mit einer CO2-Konzentration von 612 ppm zu rechnen.
Erläuterung der Lösung
AufgabenstellungBerechne die CO2-Konzentration, die laut Ihrem Modell im Jahr 2100 zu erwarten ist.
Lösung\(k(2100)=2,48\cdot2100-4596=612\)
Laut Modell ist im Jahr 2100 mit einer CO2-Konzentration von 612 ppm zu rechnen.
Teilaufgabe d)
Erwartungshorizont (offiziell)
Es ist nicht gesichert, dass sich die CO2-Konzentration bis zum Ende des Jahrhunderts weiterhin wie im Zeitraum 2012 bis 2022 entwickelt. Insbesondere könnten Klimaschutzmaßnahmen oder deren Ausbleiben dazu beitragen, dass sich der gesamte Verlauf der CO2-Konzentration grundsätzlich ändert.Erläuterung der Lösung
AufgabenstellungDeute im Sachzusammenhang, warum ein mathematisches Modell, das auf Messungen innerhalb der Jahre 2012 bis 2022 beruht, nicht grundsätzlich für eine Vorhersage der CO2-Konzentration im Jahr 2100 verwendet werden kann.
LösungEs ist nicht gesichert, dass sich die CO2-Konzentration bis zum Ende des Jahrhunderts weiterhin wie im Zeitraum 2012 bis 2022 entwickelt. Insbesondere könnten Klimaschutzmaßnahmen oder deren Ausbleiben dazu beitragen, dass sich der gesamte Verlauf der CO2-Konzentration grundsätzlich ändert.
Zusätzlich könnte man einwenden, dass eine Prognose 78 Jahre in die Zukunft basierend auf Daten eines Jahrzehnts in den meisten Fällen nicht solide ist, zum Beispiel aufgrund von Messfehlern, die sich fortpflanzen.Teilaufgabe e)
Erwartungshorizont (offiziell)
Nur \(f\) und \(j\) sind additiv verknüpfte Funktionen aus je einer trigonometrischen Funktion und einer linearen Funktion.
Die Periode \(p\) des trigonometrischen Anteils kann berechnet werden:
Funktion \(f: p_f=\frac{2\pi}{0,53}\approx11,9;\)
Funktion \(j: p_j=\frac{2\pi}{1,29}\approx4,9\)
Erläuterung der Lösung
Aufgabenstellung
Der Verlauf der monatlichen Mittelwerte der CO2-Konzentration ist für die Jahre 2019 bis 2022 in der Abbildung dargestellt. Darin sind neben einem langfristigen Trend auch die Schwankungen innerhalb eines Jahres zu erkennen.
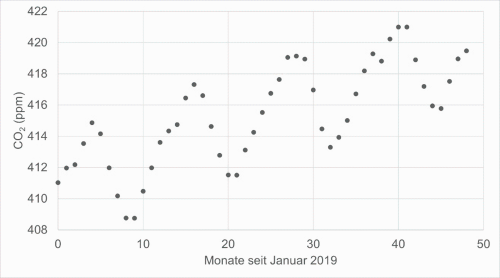Entscheide, welche der folgenden Funktionen den abgebildeten Zusammenhang am besten wiedergibt. Begründe deine Auswahl.
\(f(x)=0,19x+2,95\cdot\sin (0,53\cdot\left(x-0,17\right))+410,7\)
\(g(x)=3,14\cdot\sin(0,53\cdot\left(x+0,14\right))+415,3\)
\(h(x)=0,21x\cdot2,84\cdot\sin(0,51\cdot\left(x-0,24\right))+411,2\)
\(j(x)=0,18x+3,09\cdot\sin(1,29\cdot\left(x-0,09\right))+409,2\)
Nur \(f\) und \(j\) sind additiv verknüpfte Funktionen aus je einer trigonometrischen Funktion und einer linearen Funktion.
Die Periode \(p\) des trigonometrischen Anteils kann berechnet werden:
Funktion \(f: p_f=\frac{2\pi}{0,53}\approx11,9;\)
Funktion \(j: p_j=\frac{2\pi}{1,29}\approx4,9\)
Im Diagramm ist zu erkennen, dass der trigonometrische Anteil eine Periode besitzt, die größer als 10 ist. Folglich gibt die Funktion \(f\) den abgebildeten Zusammenhang am besten wieder.
Hinweis: Eine alleinige Untersuchung des (vermeintlichen) y-Achsenabschnitts ist nicht ausreichend und teilweise sogar irreführend.