Zum Inhalt springen

Tipp Aufgabe 1

Zuletzt geändert von akukin am 2025/01/24 14:58

Teilaufgabe a)

Hinweis Der Parameter a kann durch eine Punktprobe, zum Beispiel mit dem Punkt \left(1\middle|-1\right), berechnet werden.

Teilaufgabe b)

Hinweis 1 Zur Bestimmung eines Tiefpunkts können die erste und zweite Ableitung herangezogen werden. Es empfiehlt sich, zuerst den Funktionsterm auszumultiplizieren.
Hinweis 2 Um eine Tiefstelle zu ermitteln, genügt es zu zeigen, dass die erste Ableitung dort Null und die zweite Ableitung positiv ist.
Hinweis 3 Für die y-Koordinate des Tiefpunkts wird die ermittelte x-Koordinate in den Funktionsterm von f eingesetzt.

Teilaufgabe c)

Hinweis 1 Zuerst muss die Wendestelle bestimmt werden. Dazu wird die zweite Ableitung Null gesetzt.
Hinweis 2 Für die Steigung der Wendetangente kann die x-Koordinate der Wendestelle in den Funktionsterm der ersten Ableitung eingesetzt werden.
Hinweis 3 Die Steigung m einer Geraden und ihr Schnittwinkel \alpha mit der x-Achse sind verknüpft:
m=\tan{(\alpha)}\ \ \ \Leftrightarrow\ \ \ \alpha=\tan^{-1}{(m)}

Teilaufgabe d)

Hinweis 1 Da der Graph von s gegenüber dem Graphen von f horizontal verschoben ist, kann f^{\prime\prime}(1) ermittelt werden, indem s^{\prime\prime}(x) an einer anderen Stelle berechnet wird.
Hinweis 2 Da der Graph von s gegenüber dem Graphen von f um \frac{4}{3} nach links verschoben ist, kann f^{\prime\prime}(1) ermittelt werden, indem s^{\prime\prime}\left(1-\frac{4}{3}\right) berechnet wird.

Teilaufgabe e)

Hinweis 1 Was wird berechnet, wenn A^\prime(u) Null gesetzt wird? (vgl. f^\prime(x)=0)
Hinweis 2 A^\prime(u_1)=0\ \ \ \Leftrightarrow\ \ \ u_1=3 sagt aus, dass u_1 die einzige Stelle ist, an der die Ableitung des Flächeninhalts Null ist.
Da an dieser Stelle die zweite Ableitung negativ ist (A^{\prime\prime}(3)<0), handelt es sich um eine …
Hinweis 3 Da an der Stelle u_1=3 die zweite Ableitung negativ ist (A^{\prime\prime}(3)<0), handelt es sich um eine Hochstelle. Da der der Flächeninhalt an den Rändern des Definitionsbereichs 0,5\le u\le3,5 jeweils kleiner ist als an der Stelle u_1=3, handelt es sich sogar um eine … Hochstelle, und der dazugehörige y-Wert ist ein … Maximum.

Teilaufgabe f)

Hinweis 1 Da die Parabel p ebenfalls die Nullstellen x=0 und x=4 haben soll, kann die Parabelgleichung in Produktform angesetzt werden.
Hinweis 2 Die Produktform lautet: p(x)=k\cdot x\cdot(x-4) mit einem noch nicht bekannten Vorfaktor k\in\mathbb{R}.
Hinweis 3 Eine Skizze/Zeichnung kann sinnvoll sein, um die Flächen zu identifizieren.
Hinweis 4 Eine Skizze/Zeichnung kann sinnvoll sein, um die Flächen zu identifizieren: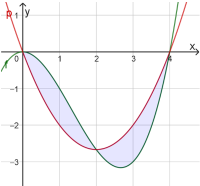 SkizzeAufgabe1f).png
Hinweis 5 SkizzeAufgabe1f).png Der Streckfaktor k der roten Parabel muss so gewählt werden, dass die beiden blauen Flächen gleich groß sind.
Hinweis 6 Ein Flächeninhalt zwischen zwei Graphen kann mittels Integralrechnung bestimmt werden. Dass dabei die Orientierung (also welcher Graph über dem anderen liegt) entscheidet, ob das Integral positiv oder negativ ist, kann hier ausgenutzt werden.
Hinweis 7 Wenn die beiden Flächen gleich groß sind, muss das Integral über die Differenz der beiden Funktionen Null ergeben:
\int_{0}^{4}{\left(f(x)-g(x)\right)\mathrm{d} x}=0

Teilaufgabe g)

Hinweis 1 h(x) kann mit Hilfe der Kettenregel abgeleitet werden.
Hinweis 2 h^\prime(x)=e^{f(x)}\cdot f^\prime(x)
Hinweis 3 h^\prime(x)=e^{f(x)}\cdot f^\prime(x)
An Extremstellen ist die erste Ableitung Null.
h^\prime(x)=0\ \ \ \Leftrightarrow\ \ \ ?
Hinweis 4 h^\prime(x)=0\ \ \ \Leftrightarrow\ \ \ e^{f(x)}\cdot f^\prime(x)=0 Benutze den Satz vom Nullprodukt.
Hinweis 5 h^\prime(x)=0\ \ \ \Leftrightarrow\ \ \ e^{f(x)}\cdot f^\prime(x)=0
Der Satz vom Nullprodukt besagt, dass dieser Term Null wird, wenn entweder e^{f(x)} oder f^\prime(x) Null wird.
Hinweis 6 h^\prime(x)=0\ \ \ \Leftrightarrow\ \ \ e^{f(x)}\cdot f^\prime(x)=0

Der Satz vom Nullprodukt besagt, dass dieser Term Null wird, wenn entweder e^{f(x)} NUll wird (was nicht eintreten kann, da Exponentialterme immer positiv sind) oder f^\prime(x) Null wird.

h^\prime und f^\prime haben also die gleichen Nullstellen. Aber sind damit auch die Arten der Extremstellen (Hoch-/Tiefstelle) gleich?