Lösung Lineare Algebra

Version 7.2 von akukin am 2025/01/24 21:42

Teilaufgabe a)

Erwartungshorizont (offiziell)

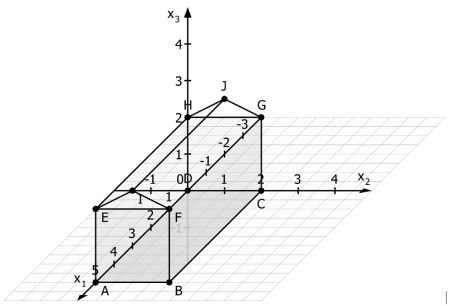
Teilaufgabe b)

Erwartungshorizont (offiziell)

$A_{BCGF}=5\cdot 2=10$
$A_{ABFE}=2\cdot 2=4$
$A_{EFI}=\frac{1}{2}\cdot 0,5\cdot 2=0,5$
$A_{FGJI}=5\cdot \sqrt{1^2+0,5^2}\approx 5,59$
$A =2\cdot (A_{BCGF}+A_{ABFE}+A_{EFI}+A_{FGJI} )=2\cdot (10+4+0,5+5,59)=40,18$
$40,18\cdot 10=401,8$
Das benötigte Glas wiegt $401,8\text{kg}$ .

Teilaufgabe c)

Erwartungshorizont (offiziell)

$\overrightarrow{JG}=\left(\begin{matrix}0\\1\\-0,5 \end{matrix}\right)$
$cos(\alpha)=\frac{\left(\begin{matrix}0\\1\\-0,5 \end{matrix}\right)\cdot \left(\begin{matrix}0\\1\\0 \end{matrix}\right)}{\sqrt{1^2+(-0,5)^2}\cdot \sqrt{1^2}}=\frac{1}{\sqrt{1,25}} \approx 0,8944 \quad \ \ \alpha \approx 26,57^\circ$

Teilaufgabe d)

Erwartungshorizont (offiziell)

Ebene

, in der das Sonnensegel liegt:
$E: \vec{x}=\overrightarrow{OF}+r\cdot \overrightarrow{FG}+ s\cdot \overrightarrow{FS}=\left(\begin{matrix}5\\2\\2 \end{matrix}\right)+ r\cdot \left(\begin{matrix}-5\\0\\0 \end{matrix}\right)+ s\cdot \left(\begin{matrix}-2\\2\\-0,5 \end{matrix}\right) \quad \ \ r,s\in \mathbb{R}$
$2+2s=3 \ \Leftrightarrow \ s=0,5$
$x_3=2-0,5\cdot 0,5=1,75<1,8 \ \text{(m)}$ (d. h. der Baumstumpf muss gekürzt werden)

Teilaufgabe e)

Erwartungshorizont (offiziell)

$\overrightarrow{FS}= \left(\begin{matrix}-2\\2\\-0,5 \end{matrix}\right); \ \ \ |\overrightarrow{FS}|=\sqrt{4+4+0,25}=\sqrt{8,25}$
$\overrightarrow{GS}= \left(\begin{matrix}3\\2\\-0,5 \end{matrix}\right); \ \ \ |\overrightarrow{GS}|=\sqrt{9+4+0,25}=\sqrt{13,25}$
$|\overrightarrow{FG}|=5$

Teilaufgabe f)

Erwartungshorizont (offiziell)

$\overrightarrow{FP_k}=\left(\begin{matrix}-2\\k-2\\-0,5 \end{matrix}\right)$
$|\overrightarrow{FP_k}|=|\overrightarrow{GF}| \ \Leftrightarrow \ 5=\sqrt{4,25+(k-2)^2 }$
0=k^2-4k-16,75