Teilaufgabe a)
Hinweis 1
\( E_1\): Die erste Person verträgt das Produkt, die zweite auch, die dritte nicht, aber alle nachfolgenden schon.Hinweis 2
\(E_2\): Die Zufallsgröße \(X\): „Anzahl der Testpersonen, die das Produkt vertragen“ ist binomialverteilt mit \(n=20\) und \(p=0,91\).Hinweis 3
\(E_3\): Zuerst muss berechnet werden, wie viel 70% von 20 Personen ist.Hinweis 4
Da der Taschenrechner nur \(P(X\leq m)\) berechnen kann, also über alle \(P(X=k)\) von \(k=0\) bis \(k=m\) aufsummiert, muss \(P(X\geq 14)\) noch umformuliert werden.
(Taschenrechner: binomialcdf)Hinweis 5
\(P(E_3)=P(X\geq 14)=1-P(X\leq 13)\approx 1- ? \approx ?\) (Taschenrechner: binomialcdf)Teilaufgabe b)
Hinweis 1
\(Y\): Anzahl der Personen, die das Produkt nicht vertragen. (Binomialverteilt mit \(n=200, \ p=0,09\))Gesucht ist \(P(14\leq Y\leq 22)\).
Hinweis 2
Da der Taschenrechner nur \(P(X\leq m)\) berechnen kann, also über alle \(P(X=k)\) von \(k=0\) bis \(k=m\) aufsummiert, muss \(P(14\leq Y\leq 22)\) noch umformuliert werden.Hinweis 3
\(P(14\leq Y\leq 22)=P(Y \leq 22)-P(Y\leq 13)\approx ?\) (Taschenrechner: binomialcdf zweimal)Teilaufgabe c)
Hinweis 1
„Bei 5,5% aller Testpersonen tritt eine Allergie auf.“| \(A\) | \(\overline{A}\) | \(\sum\) | |
| \(I\) | |||
| \(\overline{I}\) | 0,91 | ||
| \(\sum\) | ? | 1 |
Hinweis 2
„Von diesen haben 90% keine Irritation“: \(P_? (?)=0,9\)| \(A\) | \(\overline{A}\) | \(\sum\) | |
| \(I\) | |||
| \(\overline{I}\) | ? | 0,91 | |
| \(\sum\) | 0,055 | 1 |
Hinweis 3
„Von diesen haben 90% keine Irritation“: \(P_A (\overline{I})=0,9\)Pfadregel: \(\textcolor{red}{P(A\cap \overline{I})= ?} \)
| \(A\) | \(\overline{A}\) | \(\sum\) | |
| \(I\) | |||
| \(\overline{I}\) | ? | 0,91 | |
| \(\sum\) | 0,055 | 1 |
Hinweis 4
„Von diesen haben 90% keine Irritation“: \(P_A (\overline{I})=0,9\)Pfadregel: \(\textcolor{red}{P(A\cap \overline{I})=P(A)\cdot P_A (\overline{I})=0,055\cdot 0,9= ?} \)
| \(A\) | \(\overline{A}\) | \(\sum\) | |
| \(I\) | |||
| \(\overline{I}\) | ? | 0,91 | |
| \(\sum\) | 0,055 | 1 |
Hinweis 5
Die restlichen Felder können mittels Summenregel berechnet werden.(„Oben plus Mitte ist gleich unten“, „Links plus Mitte ist gleich rechts“)
| \(A\) | \(\overline{A}\) | \(\sum\) | |
| \(I\) | 0,0055 | ? | ? |
| \(\overline{I}\) | 0,0495 | 0,91 | ? |
| \(\sum\) | 0,055 | ? | 1 |
Teilaufgabe d)
Hinweis
Die stochastische (Un)abhängigkeit lässt sich auf zwei Arten überprüfen.
Option 1: Vergleich der bedingten und unbedingten Wahrscheinlichkeiten
Wenn \(P_I (A)=P(A)\), dann spielt die Bedingung \(I\) anscheinend keine Rolle; folglich sind beide Merkmale unabhängig voneinander.
Wenn \(P(A\cap I)=P(A)\cdot P(I)\), dann sind beide Merkmale unabhängig voneinander (siehe Merkhilfe).
Teilaufgabe e)
Hinweis 1
Die Formulierung „entweder … oder …“ ist nicht zu verwechseln mit dem einfachen „oder“, bei dem der Additionssatz angewendet werden kann.Hinweis 2
Während beim Additionssatz die Schnittmenge \(A\cap I\) einmal mitgezählt wird (und ihre Wahrscheinlichkeit einmal abgezogen wird, damit sie nicht fälschlicherweise doppelt gezählt wird), kommt die Schnittmenge \(A\cap I\) bei „entweder … oder …“ überhaupt nicht vor.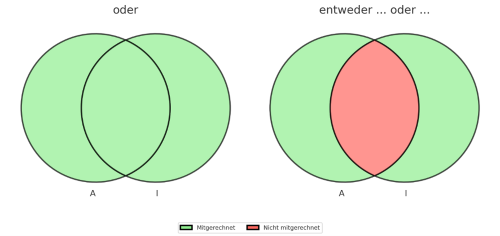
Hinweis 3
Gesucht ist die Wahrscheinlichkeit, dass eine Allergie, aber keine Irritation auftritt, addiert zur Wahrscheinlichkeit, dass eine Irritation, aber keine Allergie auftritt.Hinweis 4
\(P((A\cap \overline{I})\cup(\overline{A} \cap I))=P(A\cap \overline{I})+P(\overline{A} \cap I)= ?\)Teilaufgabe f)
Hinweis 1
Die Irritation ist schon aufgetreten; sie ist also die Bedingung.Hinweis 2
\(A\): Allergie; \(I\): IrritationDie Irritation ist schon aufgetreten; sie ist also die Bedingung.
\(P_I (A)=\frac{P(A\cap I)}{P(I)}= ?\)
Teilaufgabe g)
Hinweis 1
Eine Tabelle zur Wahrscheinlichkeitsverteilung kann hier behilflich sein.Hinweis 2
In einer Tabelle zur Wahrscheinlichkeitsverteilung werden die Werte der Zufallsgröße (hier z. B. der Gewinn) und die dazugehörigen Wahrscheinlichkeiten für alle Ereignisse notiert.Hinweis 3
In der Tabelle kann unterschieden werden zwischen „keine Rückgabe“, „Rückgabe aufgrund von Unverträglichkeit“ und „Rückgabe aus sonstigen Gründen“Zufallsvariable \(G\): Gewinn bzw. Verlust für das Unternehmen
\(a\): Anteil aller Kunden, die eine Rückerstattung aus sonstigen Gründen beantragen
| keine Rückgabe | Rückgabe aufgrund von Unverträglichkeit | Rückgabe aus sonstigen Gründen | |
|---|---|---|---|
| \(G_i\) | |||
| \(P(G=G_i)\) | \(a\) |
Hinweis 4
| keine Rückgabe | Rückgabe aufgrund von Unverträglichkeit | Rückgabe aus sonstigen Gründen | |
|---|---|---|---|
| \(G_i\) | \(9\) | \(-0,5\) | ? |
| \(P(G=G_i)\) | ? | \(0,09\) | \(a\) |
Hinweis 5
Der erwartete Gewinn soll 6,50 € sein. Aus der Formel für den Erwartungswert (siehe Merkhilfe) ergibt sich eine Gleichung für \(a\).Hinweis 6
\(\mu =\sum\limits_{i=1}^n P(X=x_i)\cdot x_i =P(X=x_1 )\cdot x_1+P(X=x_2 )\cdot x_2+\dots+P(X=x_n )\cdot x_n\)Hinweis 7
| keine Rückgabe | Rückgabe aufgrund von Unverträglichkeit | Rückgabe aus sonstigen Gründen | |
|---|---|---|---|
| \(G_i\) | \(9\) | \(-0,5\) | \(-0,5\) |
| \(P(G=G_i)\) | \(0,91 -a\) | \(0,09\) | \(a\) |
\(\mu=6,50\)
