Lösung Erkunden - Graph und Asymptoten (gerader Parameter)

a) Die Funktion \(f\) hat den maximalen Definitionsbereich \(\bold{D}=\mathbb{R}\) mit zugehörigem Wertebereich \(\bold{W}=\mathbb{R}_{0}^{+}\) (roter Graph).
Die Funktion \(g\) hat den maximalen Definitionsbereich \(\bold{D}=\mathbb{R}_{0}^{+}\) mit zugehörigem Wertebereich \(\bold{W}=\mathbb{R}_{0}^{+}\) (blauer Graph).
Die Funktion \(h\) hat den maximalen Definitionsbereich \(\bold{D}=\mathbb{R}\setminus\lbrace 0 \rbrace\) mit zugehörigem Wertebereich \(\bold{W}=\mathbb{R}^{+}\) (grüner Graph).

b) Die Graphen K_f (rot) und K_g (blau) haben keine Asymptoten; der Graph K_h (grün) hingegen hat die x-Achse als waagrechte Asymptote und die y-Achse als senkrechte Asymptote.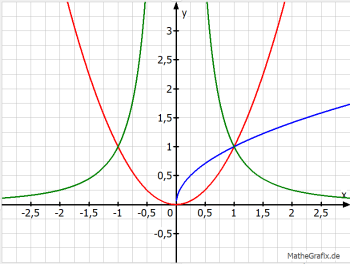

c)  Man erkennt, dass die Graphen K_f und K_h achsensymmetrisch zur y-Achse sind (nur gerade Hochzahlen im Funktionsterm).

Außerdem kann man sehen, dass der Graph K_f im 1. Quadranten und der Graph K_g spiegelsymmetrisch zur 1. Winkelhalbierenden (Gleichung \(y=x\)) sind.

Vorgriff Jahrgangsstufe 1: Die Funktionen \(f\) und \(g\) sind Umkehrfunktionen zueinander.