BPE 2.2 Transformationen

Version 86.1 von Niklas Wunder am 2024/12/17 14:14

Inhalt

AFB I Terme bestimmen Transformationen von Funktionsgraphen beschreiben
AFB II Potenzfunktionen verschieben Funktionsterme nach Transformationen bestimmen
AFB III Spiegeln an der Winkelhalbierenden

Kompetenzen

K1 K4 Ich kann anhand von Funktionstermen beschreiben, wie ein Graph mittels Transformationen – unter Berücksichtigung der Reihenfolge – aus dem Graphen der unten aufgeführten Funktionen entsteht
K1 K4 Ich kann anhand von Funktionsgraphen beschreiben, wie ein Graph mittels Transformationen – unter Berücksichtigung der Reihenfolge – aus dem Graphen der unten aufgeführten Funktionen entsteht
K4 Ich kann zu einer verbal gegebenen Transformation den zugehörigen Funktionsterm angeben
K4 Ich kann zu einer grafisch gegebenen Transformation den zugehörigen Funktionsterm angeben
f(x) = x^2
$f(x) = \frac{1}{x}$
$f(x) = \sqrt{x}$

Aufgabe 1 Terme bestimmen 𝕃

Die Funktionen f, g und h sind verschobene Potenzfunktionen mit den zugehörigen Schaubildern K_f, K_g und K_h. Bestimme die jeweiligen Funktionsterme.

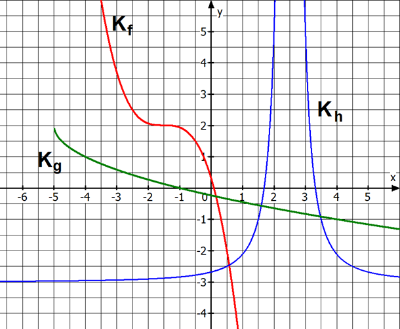
AFB I	Kompetenzen K4	Bearbeitungszeit 6 min
Quelle k.A.		Lizenz CC BY-SA

Aufgabe 2 Potenzfunktionen verschieben 𝕃

Die Funktionen f, g und sind verschobene Potenzfunktionen mit den zugehörigen Schaubildern K_f, K_g und K_h. Beschreibe wie die verschobenen Potenzfunktionen aus den ursprünglichen Funktionen hervorgehen.

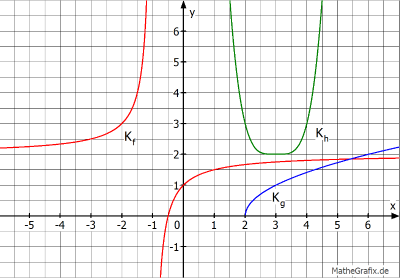
AFB II	Kompetenzen K1 K4	Bearbeitungszeit 8 min
Quelle Niklas Wunder		Lizenz CC BY-SA

Aufgabe 3 Transformationen von Funktionsgraphen beschreiben 𝕃

Beschreibe, wie die Schaubilder der nachfolgenden Funktionen jeweils aus dem Graphen $y=x^k; k \in \mathbb{Q}$ entstanden sind.
a) f(x)=6x^4-1
b) $f(x)=-\frac{1}{2}(x-5)^4-3$
c) $f(x)=\frac{1}{(x+3)^2}-8$
d) $f(x)=-4\,\sqrt[3]{x+1}+5$

AFB I	Kompetenzen K1 K4	Bearbeitungszeit 6 min
Quelle Martin Stern		Lizenz CC BY-SA

Aufgabe 4 Funktionsterme nach Transformationen bestimmen 𝕃

Bestimme jeweils einen passenden Funktionsterm.

a) Der Graph von K_f entsteht aus dem Graphen $f(x)=\frac{1}{x}$ durch Spiegelung an der x-Achse, Streckung mit dem Faktor 2 in y-Richtung sowie durch Verschiebung um 1 nach rechts und um 3 nach oben.

b) Der Graph von K_f entsteht aus dem Graphen $f(x)=\frac{1}{x}$ durch Verschiebung um 1 nach rechts und um 3 nach oben, Streckung mit dem Faktor 2 in y-Richtung sowie Spiegelung an der x-Achse.

AFB II	Kompetenzen K4	Bearbeitungszeit 8 min
Quelle Martin Stern		Lizenz CC BY-SA

Aufgabe 5 Spiegeln an der Winkelhalbierenden

Neben der Spiegelung an der x- und y- Achse kann man auch an der ersten Winkelhalbierenden (gegeben durch y=x) einen Funktionsgraphen spiegeln. Für alle Funktionen schränkt man den Definitionsbereich auf x> 0 ein. Wieso dies sinnvoll ist wird später klar. Um die Funktionsgleichung nach Spiegelung rechnerisch zu ermitteln nimmt man die Funktionsgleichung, z.B. y=x^2 , löst diese nach x auf und vertauscht anschließend die Variablen so erhält man den gespiegelten Funktionsgraphen mit passender Funktionsgleichung.

$\begin{align*} y=x^2 \;\; | \,\sqrt{\phantomtext}\\ x=\sqrt{y}\;\;$
Vertausche x und y miteinander um die Funktionsgleichung des gespiegelten Funktionsgraphens zu erhalten.
$y=\sqrt{x} \end{align*}$

Bestimme die an der ersten Winkelhabierenden gespiegelten Funktionen $f(x)=\frac{1}{x}; g(x)= \frac{1}{x^2}$ und $h(x)= \frac{2\,x+3}{-4\,x-2}$ . Hinweis:
Bestimme graphisch den an der ersten Winkelhalbierenden gespiegelten Graphen zu den drei dargestellten Graphen.
Die in a) berechneten Funktionen nennt man auch Umkehrfunktionen (Abkürzung $f^{-1}$ ) . Berechne den Funktionsterm $f^{-1}(f(x))$ . Beschreibe deine Beobachtung. Hinweis: Setze dazu den Term der Funktionsgleichung in die in a) berechnete Umkehrfunktion $f^{-1}$ ein und fasse zusammen.
1.Begründe mit Hilfe deiner Lösungen von a) und b) wieso der Definitionsbereich der Funktion verkleinert werden muss, wenn man die Funktionsgleichung der Umkehrfunktion berechnet.